
题目列表(包括答案和解析)
2.若函数f(x)=(1+tanx)cosx,0≤x<,则f(x)的最大值为 ( )
A.1 B.2 C.+1 D.+2
解析:f(x)=(1+tanx)cosx=cosx+sinx
=2sin(x+),
∵0≤x<,∴f(x)max=2.
答案:B
1.已知α∈(,π),sinα=,则tan(α+)等于 ( )
A. B.7 C.- D.-7
解析:由α∈(,π),sinα=,得tanα=-,tan(α+)==.
答案:A
20.(本题14分)已知△ABC的面积S满足≤S≤3,且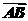 ·
·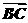 =6,AB与BC的夹
=6,AB与BC的夹
角为θ.
(1)求θ的取值范围;
(2)求函数f(θ)=sin2θ+2sinθcosθ+3cos2θ的最小值.
解:(1)由题意知:
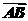 ·
·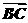 =|
=|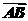 ||
||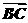 |cosθ=6,
①
|cosθ=6,
①
S=|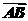 ||
||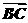 |sin(π-θ)
|sin(π-θ)
=|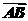 ||
||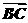 |sinθ,
②
|sinθ,
②
②÷①得=tanθ,即3tanθ=S.
由≤S≤3,得≤3tanθ≤3,即≤tanθ≤1.
又θ为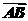 与
与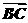 的夹角,
的夹角,
∴θ∈[0,π],∴θ∈[,].
(2)f(θ)=sin2θ+2sinθcosθ+3cos2θ
=1+sin2θ+2cos2θ
=2+sin2θ+cos2θ
=2+sin(2θ+).
∵θ∈[,],∴2θ+∈[,].
∴当2θ+=,θ=时,f(θ)取最小值3.
19.(本小题满分14分)已知A(-1,0),B(0,2),C(-3,1),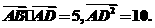
(1)求D点坐标;
(2)若D点在第二象限,用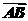 ,
,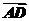 表
表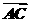 ;
;
(3)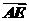 =(m,2),若3
=(m,2),若3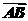 +
+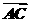 与
与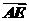 垂直,求
垂直,求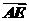 坐标.
坐标.
解:(1)设D(x,y),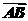 =(1,2),
=(1,2),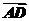 =(x+1,y).
=(x+1,y).
由题得
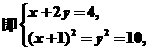
∴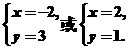
∴D点坐标为(-2,3)或(2,1).
(2)∵D点在第二象限,∴D(-2,3).
∴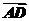 =(-1,3).∵
=(-1,3).∵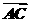 =(-2,1),
=(-2,1),
设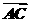 =m
=m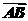 +n
+n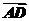 ,
,
则(-2,1)=m(1,2)+n(-1,3),
∴ ∴
∴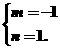
∴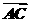 =-
=-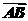 +
+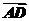 .
.
(3)∵3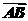 +
+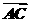 =3(1,2)+(-2,1)=(1,7),
=3(1,2)+(-2,1)=(1,7),
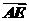 =(m,2),
=(m,2),
∴(3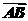 +
+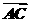 )·
)·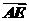 =0.
=0.
∴m+14=0.∴m=-14.
∴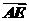 =(-14,2).
=(-14,2).
18.(本小题满分14分)已知复数z1=cosα+isinα,z2=cosβ+isinβ,|z1-z2|=.
(1)求cos(α-β)的值;
(2)若-<β<0<α<,且sinβ=-,求sinα的值.
解:(1)∵z1-z2=(cosα-cosβ)+i(sinα-sinβ),
|z1-z2|=,
∴=,
∴cos(α-β)==.
(2)∵-<β<0<α<,
∴0<α-β<π.由(1)得cos(α-β)=,
∴sin(α-β)=.又sinβ=-,∴cosβ=.
∴sinα=sin[(α-β)+β]
=sin(α-β)cosβ+cos(α-β)sinβ
=×+×(-)=.
17.(本小题满分14分)已知△ABC的角A、B、C所对的边分别是a、b、c,设向量m=(a,b),n=(sinB,sinA),p=(b-2,a-2).
(1)若m∥n,求证:△ABC为等腰三角形;
(2)若m⊥p,边长c=2,角C=,求△ABC的面积.
解:(1)证明:∵m∥n,∴asinA=bsinB,
即a·=b·,
其中R是△ABC外接圆半径,∴a=b.
∴△ABC为等腰三角形.
(2)由题意可知m·p=0,即a(b-2)+b(a-2)=0.
∴a+b=ab.
由余弦定理可知,4=a2+b2-ab=(a+b)2-3ab,
即(ab)2-3ab-4=0.
∴ab=4(舍去ab=-1),
∴S=absinC=×4×sin=.
16.(本小题满分12分)已知|a|=1,|b|=,
(1)若a与b的夹角为,求|a+b|;
(2)若a-b与a垂直,求a与b的夹角.
解:(1)|a+b|2=|a|2+2a·b+|b|2
=1+2×1××cos+2
=3+.
∴|a+b|=.
(2)∵a-b与a垂直,∴(a-b)·a=0.
∴|a|2-a·b=0,∴a·b=|a|2.
设a与b的夹角为θ.
∴cosθ====.
又0≤θ≤π,∴θ=.
所以向量a与b的夹角为.
15.(本小题满分12分)设a=(-1,1),b=(4,3),c=(5,-2),
(1)求证a与b不共线,并求a与b的夹角的余弦值;
(2)求c在a方向上的投影.
解:(1)∵a=(-1,1),b=(4,3),且-1×3≠1×4,
∴a与b不共线.
又a·b=-1×4+1×3=-1,|a|=,|b|=5,
∴cos〈a,b〉===-.
(2)∵a·c=-1×5+1×(-2)=-7,
∴c在a方向上的投影为==-.
14.(2009·四川高考)设V是已知平面M上所有向量的集合,对于映射f:V→V,a∈V,记a的象为f(a).若映射f:V→V满足:对所有a、b∈V及任意实数λ、μ都有f(λa+μb)=λf(a)+μf(b),则f称为平面M上的线性变换.现有下列命题:
①设f是平面M上的线性变换,a、b∈V,则f(a+b)=f(a)+f(b);
②若e是平面M上的单位向量,对a∈V,设f(a)=a+e,则f是平面M上的线性变换;
③对a∈V,设f(a)=-a,则f是平面M上的线性变换;
④设f是平面M上的线性变换,a∈V,则对任意实数k均有f(ka)=kf(a).
其中的真命题是 (写出所有真命题的编号).
解析:①当λ=μ=1时,f(a+b)=f(a)+f(b)成立.
②∵f(a)=a+e,∴f(λa+μb)=λa+μb+e.
λf(a)+μf(b)=λ(a+e)+μ(b+e)=λa+μb+(λ+μ)e.
f(λa+μb)≠λf(a)+μf(b).
∴f不是平面M上的线性变换.
③∵f(a)=-a,∴f(λa+μb)=-λa-μb,
λf(a)=-λa,μf(b)=-μb.
∴f(λa+μb)=λf(a)+μf(b).
∴f是平面M上的线性变换.
④∵f是M上的线性变换,∴当λ=k,μ=0时,有f(λa+μb)=f(ka)=kf(a)+0f(b)=kf(a).
答案:①③④
13.已知|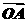 |=1,|
|=1,|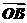 |=,
|=,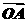 ·
·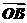 =0,点C在∠AOB内,且∠AOC=30°,设
=0,点C在∠AOB内,且∠AOC=30°,设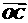 =mOA+n
=mOA+n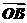 (m、n∈R),则等于
.
(m、n∈R),则等于
.
 解析:如图所示,建立直角坐标系.
解析:如图所示,建立直角坐标系.
则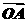 =(1,0),
=(1,0),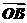 =(0,),
=(0,),
∴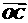 =m
=m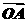 +n
+n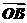
=(m,n),
∴tan30°==,
∴=3.
答案:3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com