12．(2010·福州模拟)关于x的方程(m+3)x²－4mx+2m－1＝0的两根异号，且负数根的绝对值比正数根大，那么实数m的取值范围是________．

解析：∵x₁x₂<0，x₁+x₂<0，

∴，解得－3<m<0.

答案：(－3,0)

11.设函数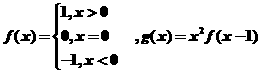 函数g(x)的递减区间是　　.

解析：依题意有g(x)=x² f(x-1)=

所以g(x)的递减区间是(0,1).

答案：(0,1)

10．函数f(x)＝x3+ax2+3x－9，已知f(x)在x＝－3时取得极值，则a＝________.

解析：因为f(x)在x＝－3时取得极值，故x＝－3是f′(x)＝3x2+2ax+3＝0的解，代入得a＝5.

答案：5

9.函数y＝log₃(9－x²)的定义域为A，值域为B，则A∩B＝　　.

解析：由9－x²>0⇒－3<x<3，

则A＝(－3,3).又0<9－x²≤9，

∴y＝log₃(9－x²)≤2，则B＝(－∞，2].

所以A∩B＝(－3,2].

答案：(－3,2]

8.当x∈[n，n+1)(n∈N)时，f(x)＝n－2，则方程f(x)＝log₂x根的个数是　　　 (　)

A.1个　 　　　B.2个　　　　　　 C.3个 　　　　　　　　D.无数个

解析：在同一坐标系中作出函数f(x)与log₂x的图象，由图可知有两个交点，因此根的个数应为2.

答案：B

第Ⅱ卷　(非选择题，共110分)

7.物体A以速度v＝3t²+1(m/s)在一直线l上运动，物体B在直线l上，且在物体A的正前方5 m处，同时以v＝10t(m/s)的速度与A同向运动，出发后物体A追上物体B所用的时间t(s)为　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.3　 　　　　　B.4　　　　　　　　　 C.5　 　　　　　　　　　D.6

解析：因为物体A在t秒内行驶的路程为∫(3t²+1)dt，

物体B在t秒内行驶的路程为∫10tdt，

所以∫(3t²+1－10t)dt＝(t³+t－5t²)|＝t³+t－5t²＝5

⇒(t－5)(t²+1)＝0，即t＝5.

答案：C

6.一张正方形的纸片，剪去两个一样的小矩形得到一个“E”形图案，如图所示，设小矩形的长、宽分别为x、y，剪去部分的面积为20，若2≤x≤10，记y＝f(x)，则y＝f(x)的图象是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

解析：由题意可知，y＝(2≤x≤10).

答案：A

5.若函数f(x)＝x³+f′(1)x²－f′(2)x+3，则f(x)在点(0，f(0))处切线的倾斜角为　　 (　)

A. 　　　　　　B.　　　　　　 C.　 　　　　　D.

解析：由题意得：f′(x)＝x²+f′(1)x－f′(2)，

令x＝0，得f′(0)＝－f′(2)，

令x＝1，得f′(1)＝1+f′(1)－f′(2)，

∴f′(2)＝1，∴f′(0)＝－1，

即f(x)在点(0，f(0))处切线的斜率为－1，

∴倾斜角为π.

答案：D

4.下列是关于函数y＝f(x)，x∈[a，b]的几个命题：

①若x₀∈[a，b]且满足f(x₀)＝0，则(x_0,0)是f(x)的一个零点；

②若x₀是f(x)在[a，b]上的零点，则可用二分法求x₀的近似值；

③函数f(x)的零点是方程f(x)＝0的根，但f(x)＝0的根不一定是函数f(x)的零点；

④用二分法求方程的根时，得到的都是近似值.

那么以上叙述中，正确的个数为　　　　　　　　　　　　　　　　　　　　　 (　)

A.0　 　　　　　B.1　　　　　　 C.3 　　　　　　　　D.4

解析：因为①中x₀∈[a，b]且满足f(x₀)＝0，则x₀是f(x)的一个零点，而不是(x_0,0)，所以①错误；

②因为函数f(x)不一定连续，所以②错误；

③方程f(x)＝0的根一定是函数f(x)的零点，所以③错误；

④用二分法求方程的根时，得到的根也可能是精确值，所以④也错误.

答案：A

3.函数f(x)＝lg的大致图象是　　　　　　　　　　　　　　　　　　　　　 (　)

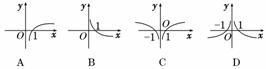
解析：∵f(x)＝lgx＝lg是偶函数，

∴A、B不正确.

又∵当x>0时，f(x)为增函数，

∴D不正确.

答案：C