2．运用比例作平行线

　例2．(如图3)四边形ABCD与ABEF是两个全等正方形，且AM=FN，其中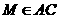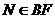，，求证：MN∥平面BCE

　解题分析：要证明MN∥平面BCE，由于在平面BCE内不易找到与MN平行的直线，因此可以考虑构造过MN的平面与平面BCE平行．

证明：因为四边形ABCD与ABEF

是两个全等正方形，且AM＝FN，

　所以CM＝BN

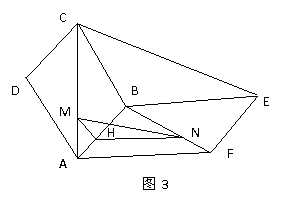　过点N作HN∥AF，连接MH，

　则有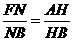

　又FN＝AM，NB＝MC

　所以＝

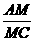
　因此HM∥BC

　　HM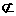平面BCE

CB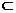平面BCE

　则有HM∥平面BCE

　同理HN∥平面BCE

　又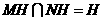

　所以平面MNH∥平面BCE

　因此MN∥平面BCE

　　解题剖析：解答此题的关键是运用比例构造平行线．但是证题时极易把M、N

　当作中点，而把MN看成是的中位线，得到MN∥CE的错误．

　运用中点做平线线是运用比例作平行线的特殊情况．

3运用传递性作平行线

　例3．求证：一条直线与两个相交平面都平行，则这条直线和它们的交线平行．

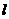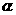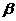　已知：(如图4)直线与平面、，有，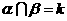

且∥，∥，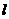　　

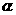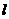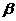　求证：∥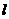

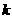
证法一：设过直线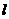的平面为、，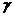

且，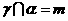　

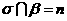
又因为∥，∥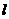

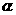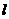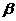
　根据直线与平面平行的性质定理有：

　∥，∥

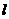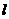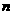
　则有∥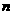，又，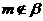

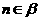
　所以∥

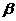
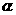　显然又有经过直线的平面为，且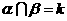

　根据直线与平面平行的性质定理有：

　　∥

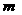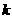
　由上可知∥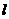

　因此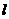∥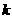得证．

解题剖析：在证题中两次运用了直线与平面平行的性质定理，把线面平行转化为了线线平行，这在证题中是经常用到的作(找)平行线的方法．

运用直线与平面平行的性质作平行线可以简述为：“过直线，作平面，找交线，则线线平行”．它揭示了直线与平面平行中蕴含着直线与直线平行，从而转化为直线与平面的平行，平面与平面的平行，同时也给出了一种作平行线的重要方法．

　4运用特殊位置作平行线

　例4．(如图5)正三棱柱ABC－A₁B₁C₁的底面边长为2，点E、F分别是C₁C­、B₁B上的点，点M是线段AC上的动点，EC＝2FB＝2．问当点M在何位置时MB∥平面AEF？　

解题分析：此题是要在平面AEF内找一直线与MB平行，经计算可得：AF＝EF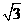＝，于是考虑构造等腰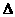AEF与等边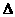ABC底边上的中线．

　解答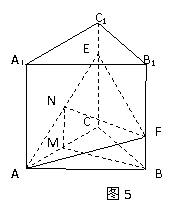： 取AC的中点M， AE的中点N，所以N为AE的中点　

　因此MN∥EC

　　且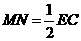

又由FB∥EC

且EC＝2FB＝2得

　所以MN∥FB，且MN＝FB

因此，FN∥MB

　　FN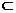平面AEF

　　MB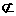平面AEF

　　所以MB∥平面AEF

　因此当点M在AC的中点时，MB∥平面AEF

　解题评注：这是一道较为简单的探索性题型，这里考虑了特殊位置较为简单的给出了平行线．在解题时需要有着较强的观察能力，简捷解题．

　可见，应用线面平行与面面平行的判定与性质解题时，都要转化为线线平行的问题，通

过观察图形根据定理与题设产生平行线是解题的关键．在学习中我们要善于挖掘定理的隐藏

条件，迅速确定解题方法．

1．运用中点作平行线

例1．已知四棱锥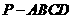的底面是距形，M、N分别是AD、PB的中点，求证MN∥平面PCD．

解题分析：要证明MN∥平面PCD，通常的方法是在平面PCD内找到一直线与MN平行；或者是过直线MN构造一平面与平面PCD平行．

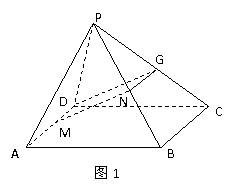证法一．(如图1)取PC的中点G，

又由于M、N分别是AD、PB的中点

所以NG∥BC，且NG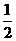＝BC

又底面ABCD为矩形

所以DM∥BC且DM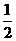＝BC

因此，DM∥NG 且DM＝NG

所以，四边形MNGD是平行四边形

MN∥DG

　MN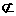平面PCD

DG平面PCD

　 因此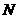，∥平面PCD

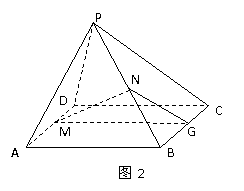证法二．(如图2)取BC的中点G

由于M、N分别是AD、PB的中点

因此，NG∥PC

NG平面PCD

PC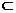平面PCD　

所以NG∥平面PCD

同理可证MG∥平面^PCD

又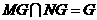

所以平面MNG∥平面PCD

因此，MN∥平面PCD

解题剖析：直线与平面平行的判断定理告诉我们，要证明线面平行，转化为证明线线平行，因此其关键是在平面内最为恰当的位置找出一条直线与该直线平行．

此题不论从哪一个角度解答，其关键是抓住了中点，从而构造三角形的中位线使问

题得到解决．

20． (本小题满分14分)(2010·东北四市模拟)已知O为坐标原点，点A、B分别在x轴，y轴上运动，且|AB|＝8，动点P满足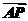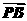＝，设点P的轨迹为曲线C，定点为M(4,0)，直线PM交曲线C于另外一点Q.

(1)求曲线C的方程；

(2)求△OPQ面积的最大值．

解：(1)设A(a,0)，B(0，b)，P(x，y)，

则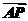＝(x－a，y)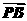，＝(－x，b－y)，

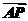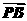∵＝，∴∴a＝x，b＝y.

又|AB|＝＝8，∴+＝1.

∴曲线C的方程为+＝1.

(2)由(1)可知，M(4,0)为椭圆+＝1的右焦点，

设直线PM方程为x＝my+4，

由消去x得

(9m²+25)y²+72my－81＝0，

∴|y_P－y_Q|＝

＝.

∴S_△OPQ＝|OM||y_P－y_Q|＝2×

＝＝＝

≤＝，

当＝，

即m＝±时，△OPQ的面积取得最大值为，此时直线方程为3x±y－12＝0.

19．(本小题满分14分)已知A、B、D三点不在一条直线上，且A(－2,0)，B(2,0)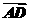，||＝2，＝(+)．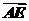

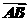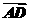(1)求E点的轨迹方程；

(2)过A作直线交以A、B为焦点的椭圆于M，N两点，线段MN的中点到y轴的距离为，且直线MN与E点的轨迹相切，求椭圆的方程．

解：(1)设E(x，y)，由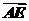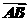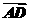＝(+)，可知E为线段BD的中点，

又因为坐标原点O为线段AB的中点，

所以OE是△ABD的中位线，

所以|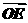|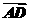＝||＝1，

所以E点在以O为圆心，1为半径的圆上，

又因为A，B，D三点不在一条直线上，

所以E点不能在x轴上，

所以E点的轨迹方程是x²+y²＝1(y≠0)．

(2)设M(x₁，y₁)，N(x₂，y₂)，中点为(x₀，y₀)，椭圆的方程为+＝1，直线MN的方程为y＝k(x+2)(当直线斜率不存在时不成立)，

由于直线MN与圆x²+y²＝1(y≠0)相切，

所以＝1，解得k＝±，

所以直线MN的方程为y＝±(x+2)，

将直线y＝±(x+2)代入方程+＝1，

整理可得：4(a²－3)x²+4a²x+16a²－3a⁴＝0，

所以x₀＝＝－.

又线段MN的中点到y轴的距离为，

即x₀＝－＝－，解得a＝2.

故所求的椭圆方程为+＝1.

18． (本小题满分14分)给定抛物线C：y²＝4x，F是C的焦点，过点F的直线l与C相交于A，B两点，记O为坐标原点．

(1)求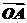·的值；

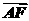(2)设＝λ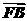，当△OAB的面积S∈[2， ]时，求λ的取值范围．

解：(1)根据抛物线的方程可得焦点F(1,0)，

设直线l的方程为x＝my+1，

将其与C的方程联立，消去x可得y²－4my－4＝0.

设A，B点的坐标分别为(x₁，y₁)，(x₂，y₂)(y₁>0>y₂)，

则y₁y₂＝－4.

因为y＝4x₁，y＝4x₂，

所以x₁x₂＝yy＝1，

故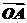·＝x₁x₂+y₁y₂＝－3.

(2)因为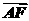＝λ，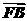

所以(1－x₁，－y₁)＝λ(x₂－1，y₂)，

即

又y＝4x₁，　　　　　　　　　　　　　　　　 　　③

y＝4x₂，　　　　　　　　　　　　　　　　　　　 ④

由②③④消去y₁，y₂后，得到x₁＝λ²x₂，将其代入①，注意到λ>0，解得x₂＝.从而可得y₂＝－，y₁＝2，

故△OAB的面积S＝|OF|·|y₁－y₂|＝+，

因+≥2恒成立，所以只要解+≤即可，

解之得≤λ≤.

17．(本小题满分14分)(2010·南通模拟)已知动圆过定点F(0,2)，且与定直线L：y＝－2相切．

(1)求动圆圆心的轨迹C的方程；

(2)若AB是轨迹C的动弦，且AB过F(0,2)，分别以A、B为切点作轨迹C的切线，设两切线交点为Q，证明：AQ⊥BQ.

解：(1)依题意，圆心的轨迹是以F(0,2)为焦点，L：y＝－2为准线的抛物线．

因为抛物线焦点到准线距离等于4，

所以圆心的轨迹是x²＝8y.

(2)证明：因为直线AB与x轴不垂直，

设AB：y＝kx+2.

A(x₁，y₁)，B(x₂，y₂)．

由

可得x²－8kx－16＝0，x₁+x₂＝8k，x₁x₂＝－16.

抛物线方程为y＝x²，求导得y′＝x.

所以过抛物线上A、B两点的切线斜率分别是k₁＝x₁，k₂＝x₂，k₁k₂＝x₁·x₂＝x₁·x₂＝－1.

所以AQ⊥BQ.

16．(本小题满分12分)过点P(2,4)作两条互相垂直的直线l₁、l₂，若l₁交x轴于A点，l₂交y轴于B点，求线段AB的中点M的轨迹方程．

解：设M的坐标为(x，y)，则A、B两点的坐标分别是(2x,0)，(0,2y)，连结PM，

∵l₁⊥l₂，∴2|PM|=|AB|.

而|PM|=，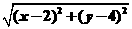

|AB|=,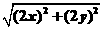

∴2.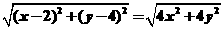

化简，得x+2y-5=0即为所求的轨迹方程．

15．(本小题满分12分)已知：圆C：x²+y²－8y+12＝0，直线l：ax+y+2a＝0.

(1)当a为何值时，直线l与圆C相切；

(2)当直线l与圆C相交于A、B两点，且AB＝2时，求直线l的方程．

解：将圆C的方程x²+y²－8y+12＝0配方得标准方程为x²+(y－4)²＝4，则此圆的圆心为(0,4)，半径为2.

(1)若直线l与圆C相切，则有＝2.

解得a＝－.

(2)过圆心C作CD⊥AB，则根据题意和圆的性质，

得

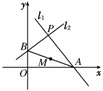解得a＝－7，或a＝－1.

故所求直线方程为7x－y+14＝0或x－y+2＝0.

14．△ABC的顶点A(－5,0)，B(5,0)，△ABC的内切圆圆心在直线x＝3上，则顶点C的轨迹方程是________

解析：如图

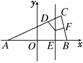|AD|＝|AE|＝8，

|BF|＝|BE|＝2，

|CD|＝|CF|，

所以|CA|－|CB|＝8－2＝6.

根据双曲线定义，所求轨迹是以A、B为焦点，实轴长为6的双曲线的右支，方程为－＝1(x＞3)．

答案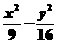：＝1(x>3)

13．若双曲线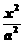－y²＝1的一个焦点为(2,0)，则它的离心率为________．

解析：由a²+1＝4，∴a＝，

∴e＝＝.

答案：