
题目列表(包括答案和解析)
3.有向线段:具有方向的线段就叫做有向线段,三个要素:起点、方向、长度.
向量与有向线段的区别:
(1)向量只有大小和方向两个要素,与起点无关,只要大小和方向相同,则这两个向量就是相同的向量;
(2)有向线段有起点、大小和方向三个要素,起点不同,尽管大小和方向相同,也是不同的有向线段.
2.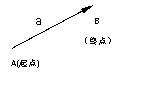 向量的表示方法:
向量的表示方法:
①用有向线段表示;
②用字母a、b(黑体,印刷用)等表示;
③用有向线段的起点与终点字母: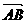 ;
;
④向量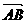 的大小――长度称为向量的模,记作|
的大小――长度称为向量的模,记作|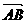 |.
|.
1、数量与向量的区别:
数量只有大小,是一个代数量,可以进行代数运算、比较大小;
向量有方向,大小,双重性,不能比较大小.
2.通过对向量的学习,初步认识现实生活中的向量和数量的本质区别.
1.了解向量的实际背景,理解平面向量的概念和向量的几何表示;掌握向量的模、零向量、单位向量、平行向量、相等向量、共线向量等概念;并会区分平行向量、相等向量和
共线向量.
4. 求取值范围
例4 已知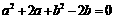 ,求
,求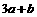 的取值范围.
的取值范围.
解:由 ,得
,得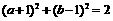 .
.
令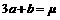 ,则点
,则点 在直线
在直线 上.
上.
 到直线
到直线 的距离
的距离 .
.
由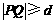 ,得
,得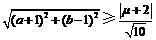 .
.
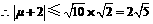 ,
,
 ,即
,即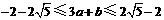 .
.
通过以上几何可以看出:在求某些代数问题时,如能联系两点距与点线距的关系,则会使问题变得直观简捷,不失为一神“巧思妙解”.
3. 求函数最值
例3 已知 满足
满足 ,求
,求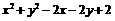 的最小值.
的最小值.
分析:本题是求二元函数的最小值问题,可以通过转化,将其化为二次函数来求解,但如果我们运用点到直线的距离,则可使求解变得更巧妙.
解:原式可化为 ,其几何意义为两点
,其几何意义为两点 和
和 间距离的平方,而点
间距离的平方,而点 在直线
在直线 上.
上.
由 两点间距离不小于
两点间距离不小于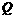 到直线
到直线 的距离,得
的距离,得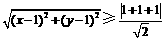 ,
,
即 .
.
 的最小值为
的最小值为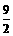 .
.
2. 证明不等式
例2 求证: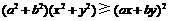 .
.
分析:本题证法很多,可利用函数、平面几何等方法.然而用解析几何知识,通过构造点到直线的距离及两点间的距离证明既直观又巧妙.
证明:设直线 ,
,
则原点与直线 上任一点的距离为
上任一点的距离为 .
.
由垂线段最短知,此距离不小于原点到直线 的距离,即
的距离,即 .
.
又 ,
,
 .
.
 .
.
1. 证明等式
例1 若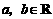 ,且
,且 .求证:
.求证: .
.
证明:由已知条件可知,
点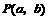 在直线
在直线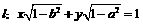 上,
上,
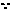 原点
原点 到直线
到直线 的距离不大于
的距离不大于 ,即
,即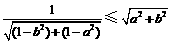 ,
,
整理,得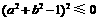 ,即
,即 .
.
方法:若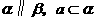 ,则
,则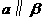 .
.
例2 如图2, 是
是 所在平面外的一点,
所在平面外的一点,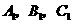 依次是
依次是
 的重心,
的重心, 是平面
是平面 内的任意一条直线,
内的任意一条直线,
求证: 平面
平面 .
.
 证明:连结
证明:连结 ,使得它们的延长线分别与
,使得它们的延长线分别与 交于点
交于点 ,连结
,连结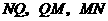 .
.
 分别是
分别是 的重心,
的重心,
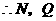 分别是
分别是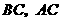 的中点.
的中点.
 是
是 的中位线,
的中位线,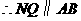 .
.
另一方面,在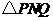 中,有
中,有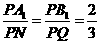 ,
,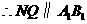 .
.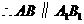 .
.
又 平面
平面 ,
, 平面
平面 ,
,
 平面
平面 ,
,
同理可证: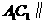 平面
平面 ,
,
又 平面
平面 ,
,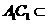 平面
平面 ,且
,且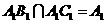 ,
,
 平面
平面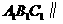 平面
平面 .
.
再由 是平面
是平面 内的任意一条直线,得
内的任意一条直线,得 平面
平面 .
.
点评:通过面面平行证明线面平行,
在本例中体现在: .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com