
题目列表(包括答案和解析)
1、平面的概念
(1)“平面”是一个只描述而不定义的最基本的概念,它与点、线一样,都是从实际生活中抽象出来的数学概念.
(2)平面的无限延展性
平面内包含着无数条直线,而直线是可以无限延伸的,因此平面也必然具有无限延展的性质.日常接触到的很多平面的实例都只是平面的一部分,用平行四边形来表示平面,也只能画出平面的一部分.
在解决球问题时,除了以上几种方法外,还应掌握一定的规律.如长方体的外接规律:长方体的外接球直径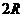 恰为其对角线长为
恰为其对角线长为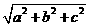 ,即
,即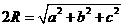 .特别地,正方体的外接球直径
.特别地,正方体的外接球直径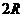 恰为其对角线长
恰为其对角线长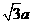 ,即
,即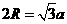 .
.
例4 已知球内接正方体的表面积为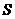 ,那么球的体积等
,那么球的体积等
于 .
解:设正方体的边长为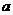 ,则有
,则有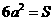 .
.
又由性质有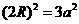 ,故有
,故有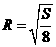 .
.
由此求得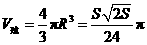 .
.
解与球有关的截面问题通常要作出轴截面,即通过大圆的截面.
例3 一平面截一球得到直径是6cm的圆面,球心到这个
平面的距离是4cm,则该球的体积是( )
A.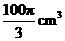 B.
B.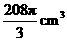
C.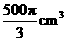 D.
D.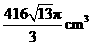
分析:作过大圆的截面,则问题可迎刃而解.
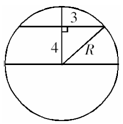 解:画出截面图,作图所示,知球的半径
解:画出截面图,作图所示,知球的半径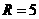 ,求得
,求得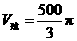 ,故选(C).
,故选(C).
评注:解有关球的表面积和体积问题,最关键是画出截面图,转化为平面几何问题求出球半径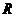 .
.
因为大圆的半径就是球的半径,所以我们可以把球的问题转化为圆的问题,使空间问题
平面化.
例2用平面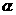 截半径的为
截半径的为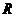 的球,如果球心到平面
的球,如果球心到平面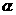 的距离为
的距离为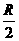 ,那么截得小圆的面积与球的表面积的比值为 .
,那么截得小圆的面积与球的表面积的比值为 .
分析:只要画出截面及球的大圆,利用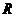 及
及 的数量关系,即可求出小圆的半径
的数量关系,即可求出小圆的半径 .
.
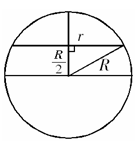 解:作出球的大圆截面图,如图所示,易得
解:作出球的大圆截面图,如图所示,易得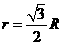 .故得
.故得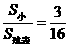 .
.
评注:展示大圆的特征图是将空间问题平面化的重要途径.对于球问题通常要抓住其特征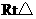 (即球半径、小圆半径及圆心距构成的直角三角形)来解决.
(即球半径、小圆半径及圆心距构成的直角三角形)来解决.
球心是球的灵魂,抓住球心就抓住了球的位置,特别是当球与球相切或球与平面相切时,我们更应该通过球心和切点及球心的连线来构造多面体,使球问题转化为多面体问题来加以解决.
例1已知球 的半径为1,
的半径为1,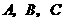 三点都在球面上,且每两点间的球面距离为
三点都在球面上,且每两点间的球面距离为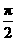 ,则球心
,则球心 到平面
到平面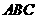 的距离为( )
的距离为( )
A.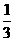 B.
B.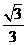 C.
C.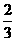 D.
D.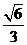
分析:突出球心 即可.由于三点
即可.由于三点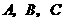 在球面上,且每两点间的球面距离相等.故可构造正三棱锥求解.
在球面上,且每两点间的球面距离相等.故可构造正三棱锥求解.
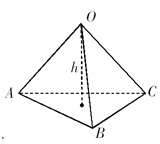 解:球心
解:球心 与
与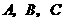 三点构成正三棱锥
三点构成正三棱锥 ,如图所示,
,如图所示,
已知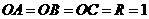 ,
,
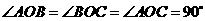 ,
,
由此可得 面
面 .
.
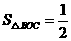 ,
,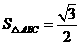 .
.
由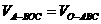 ,得
,得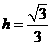 .故选(B).
.故选(B).
评注:解有关球面距离的问题,最关键是突出球心,找出数量关系.
8.已知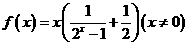 ,
,
⑴判断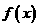 的奇偶性;
⑵证明
的奇偶性;
⑵证明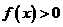 .
.
7.若函数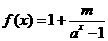 是奇函数,则
是奇函数,则 为__________。
为__________。
6.若函数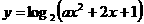 的值域为
的值域为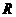 ,则
,则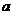 的范围为__________。
的范围为__________。
5.若函数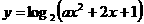 的定义域为
的定义域为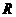 ,则
,则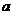 的范围为__________。
的范围为__________。
4.设函数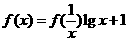 ,则
,则 的值为
的值为
A.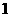 B.
B.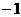 C.
C. D.
D.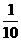
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com