8．两平行线间的距离：本类问题常见的有两种解法：①转化为点到直线的距离问题，在任一条直线上任取一点，此点到另一条直线的距离即为两直线之间的距离；②距离公式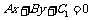：直线与直线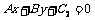的距离为．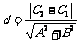

7．解题思路的比较与选择：在推导点到直线的距离公式时，课本首先给出了一个非常自然的直接的思路，然后应用另外一种思路即面积法推导公式，这是一种非常巧妙的间接的方法．在我们今后的解题过程中，很多时候都会想到一些看起来非常自然的思路，但往往思路简单而运算过程却很繁琐。因此，在学习过程中，每遇到一类问题，我们都要把各种思路进行对比、总结，找出解决问题的最简单的思路和方法，以便以后在类似的问题中套用．

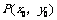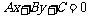6．点到直线的距离公式：点到直线的距离为．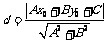

此公式常用于求三角形的高、两平行间的距离及下一章中直线与圆的位置关系的判断等．点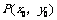到直线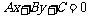的距离为直线上所有的点到已知点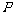的距离中最小距离．

5．应用解析思想解决问题的基本步骤：

第一步：建立适当的坐标系，用坐标表示有关的量．坐标系的选择是否适当是影响解题过程简捷与否的重要因素，坐标系建立的不恰当会人为的扩大题目的计算量．在建立坐标系时一般以特殊的点、线作为坐标系的原点和坐标轴，如课本116页例4中，以平行四边形的一个顶点作为原点，一边所在的直线为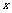轴建立直角坐标系．建立坐标系时，对图形的特性应用的越充分，题目中出现的变量就会越少，运算过程也会越简便．

第二步：进行有关的代数运算．通过各点的坐标、各图形方程之间的各种运算，求得所需结果的代数形式．通过运算可求得各个点、直线间的距离、角度、直线的斜率、截距、直线方程及两直线的交点等．如课本113页例1中，通过解方程组来求两直线的交点，课本116页例4中，多次应用两点间的距离公式计算平行四边形的对角线的长度等．

第三步：把代数运算结果“翻译”成几何关系．通过计算结果说明某几何结论成立．如课本114页例2(2)中，通过方程组无解，说明两直线为平行关系．

4．两点间的距离公式：两点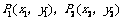间的距离公式为

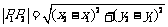．此公式可以用来求解平面上任意两点之间的距离，它是所有求距离问题的基础，点到直线的距离和两平行直线之间的距离均可转化为两点之间的距离来解决．另外在下一章圆的标准方程的推导、直线与圆、圆与圆的位置关系的判断等内容中都有广泛应用，需熟练掌握．

3．过两直线交点的直线系方程：如果两直线与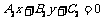相交，则方程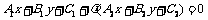为过其交点的一系列直线的方程，当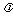取遍所有实数时，此直线系包含了除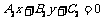直线之外过直线与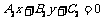的交点的所有直线方程．

2．直线的交点：求两直线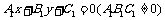与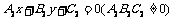的交点坐标，只需求两直线方程联立所得方程组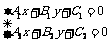的解即可．若有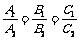，则方程组有无穷多个解，此时两直线重合；若有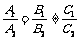，则方程组无解，此时两直线平行；若有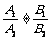，则方程组有唯一解，此时两直线相交，此解即两直线交点的坐标．

1．解析的基本思想：通过建立坐标系和图形的方程，用代数的方法对几何问题进行定量的研究，此即解析的基本思想．本章通过直线方程，用代数的方法来解决两直线的交点、位置关系、两点间的距离、点到直线的距离及两平行直线间距离等问题．

9．要注意培养空间意识

　同学们在复习立体几何时要有一个意识，即立体几何是平面几何的“升级”．在复习中要有意识地将平面几何中的“点、线、面”问题“升级”为立体几何中的“线、面、体”问题，养成这种意识，对以后的空间意识的学习习惯的养成是很有帮助的．

8．注意“降维”思想的应用，将空间的问题转化为平面内的问题，将已知条件与所求结论集中到同一个平面内，很多关系就容易发现了．