
题目列表(包括答案和解析)
4.平面与平面平行的性质定理指出了两个平面平行时所具有的性质.由平面与平面平行的定义及直线和平面平行的定义可知:两个平面平行,其中一个平面内的直线必平行于另一个平面.不仅空间平行线具有传递性,而且空间的平行平面也具有传递性,即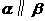 ,
, .
.
3.平面与平面平行的判定定理需五个条件,用符号语言表示为: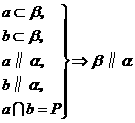 .
.
2.直线和平面平行的性质定理用符号语言来表示,即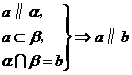 .其实质是:已知线面平行,过已知直线作一平面和已知平面相交,其交线必和已知直线平行.
.其实质是:已知线面平行,过已知直线作一平面和已知平面相交,其交线必和已知直线平行.
1.在应用直线和平面平行的判定定理判断线面平行时,必须满足三个条件:①直线 在已知平面外(
在已知平面外(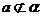 );②直线
);②直线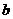 在已知平面内(
在已知平面内(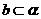 );③两直线平行(
);③两直线平行(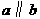 ).这三个条件是缺一不可的.其实质是:对于平面外的一条直线,只需在平面内找出一条直线和这条直线平行,就可断定这条直线必和这个平面平行.
).这三个条件是缺一不可的.其实质是:对于平面外的一条直线,只需在平面内找出一条直线和这条直线平行,就可断定这条直线必和这个平面平行.
应用以上定理证明立体几何问题,是本节的核心内容之一.定理的应用,具有较强的规律性,现总结如下,供同学们在学习中参考:
见到已知想性质,见到结论找依据,发展已知,转化结论,沟通已知和未知的关系;辅助线,辅助面是沟通的有效手段,性质和判定的转化,体现着对立和统一.
它们之间的相互关系可用下图表示:
线线垂直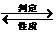 线面垂直
线面垂直 面面垂直
面面垂直
 判定定理:若一个平面经过另一个平面的一条垂线,则这两个平面垂直.符号表示为:
判定定理:若一个平面经过另一个平面的一条垂线,则这两个平面垂直.符号表示为:
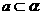 ,
,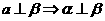 .
.
该定理可简记为:
线面垂直 面面垂直.由此定理,要证明两个平面垂直,只需要在一个平面内找到或作出一条直线与另一个平面垂直即可.
面面垂直.由此定理,要证明两个平面垂直,只需要在一个平面内找到或作出一条直线与另一个平面垂直即可.
 性质定理:两个平面垂直,则在一个平面内垂直于交线的直线与另一个平面垂直.
性质定理:两个平面垂直,则在一个平面内垂直于交线的直线与另一个平面垂直.
符号表示为: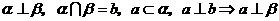 .
.
该定理可简记为:面面垂直?圯线面垂直.它给出了证明线面垂直的一种方法.
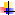 判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.符
判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直.符
号表示为: 该定理可简记为:线线垂直
该定理可简记为:线线垂直 线面垂直.根据这一定理,要证明一条直线和一个平面垂直,只需要在这个平面内找到两条相交直线与这条直线垂直即可.从而将原本判定直线与平面垂直的问题,转化为判定直线和直线垂直的问题.在应用该定理的过程中,要注意这两条直线“在平面内”和“相交”这两个条件.
线面垂直.根据这一定理,要证明一条直线和一个平面垂直,只需要在这个平面内找到两条相交直线与这条直线垂直即可.从而将原本判定直线与平面垂直的问题,转化为判定直线和直线垂直的问题.在应用该定理的过程中,要注意这两条直线“在平面内”和“相交”这两个条件.
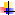 性质定理:垂直于同一个平面的两直线平行.符号表示为:
性质定理:垂直于同一个平面的两直线平行.符号表示为: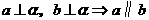 .
.
该定理可简记为:线面垂直 线线平行.它给出了判定两条直线平行的又一种方法.
线线平行.它给出了判定两条直线平行的又一种方法.
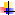 直线和平面垂直:如果一条直线和一个平面内的任意一条直线都垂直,我们就说这条
直线和平面垂直:如果一条直线和一个平面内的任意一条直线都垂直,我们就说这条
直线和这个平面垂直.这条直线叫平面的垂线,这个平面叫直线的垂面,它们的交点叫作垂足,垂线上任意一点到垂足间的线段叫作这个点到这个平面的垂线段.
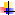 二面角:平面内的一条直线,把这个平面分为两部分,其中的每一部分叫做半平面,
二面角:平面内的一条直线,把这个平面分为两部分,其中的每一部分叫做半平面,
从一条直线出发的两个半平面组成的图形叫做二面角.
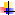 平面与平面垂直:两个平面相交,如果它们所成的二面角是直二面角,我们就说这两
平面与平面垂直:两个平面相交,如果它们所成的二面角是直二面角,我们就说这两
个平面垂直.
3.补充说明:
(1)在应用两点式求直线方程时,往往把分式形式通过交叉相乘转化为整式形式,从而得到的方程中,包含了x1=x2或y1=y2的情况,但此转化过程不是一个等价的转化过程,不能因此忽略由x1、x2和y1、y2是否相等引起的讨论.要避免讨论,可直接假设两点式的整式形式.
(2)截距相等问题中,勿忽略a=b=0即直线过原点时的情况.
(3)若两点P1(x1,y1)、P2(x2,y2),其中点为(x,y),则x= ,y=
,y=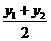 ,称为中点公式,需熟练掌握.
,称为中点公式,需熟练掌握.
(4)某点关于各轴及任意直线的对称点的坐标的求法需熟悉;有关光线的反射问题,最终都需转化为对称问题来解决.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com