
题目列表(包括答案和解析)
13.如下图,用长为l的木条围成上部分是半圆下部分是矩形的窗框,中间有2根横档,要使透光效果最好,应如何设计?
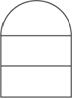
解析:设半圆的半径为x,则窗户的面积y=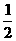 πx2+2x·
πx2+2x·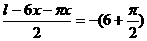 x2+l x,
x2+l x,
由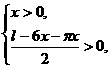
解得0<x<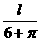 .
.
∴y=-(6+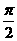 )x2+lx(0<x<
)x2+lx(0<x<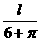 ).
).
当x=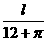 时y有最大值.这时半圆的直径为
时y有最大值.这时半圆的直径为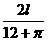 ,大矩形的另一边长为
,大矩形的另一边长为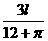 .
.
12.已知函数f(x)=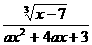 的定义域为R,求a的取值范围.
的定义域为R,求a的取值范围.
解析:当a=0时,函数定义域为R.
当a≠0时,要使ax2+4ax+3≠0对一切x∈R恒成立,其充要条件是Δ<0,即16a2-12a<0,∴0<a< .
.
因此a的取值范围为[0, ).
).
11.已知函数f(x+a)=|x-2|-|x+2|,且f[f(a)]=3,求a的值.
解析:令x=0,f(a)=|-2|-|2|=0.
∴f[f(a)]=f(0)=|-a-2|-|-a+2|=3.
∴|a+2|-|a-2|=3.
当a>2时,有a+2-(a-2)=3无解;
当-2≤a≤2时,有a+2+(a-2)=3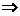 a=
a=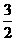 ;
;
当a≤-2时,有-(a+2)+(a-2)=3无解.
∴a=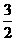 .
.
10.设函数f(x)=logax(a>0且a≠1),函数g(x)=-x2+bx+c且f(2+ )-f(
)-f( +1)=
+1)=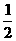 ,g(x)的图象过点A(4,-5)及B(-2,-5),则a=____________;函数f[g(x)]的定义域为_______________.
,g(x)的图象过点A(4,-5)及B(-2,-5),则a=____________;函数f[g(x)]的定义域为_______________.
答案:2 -1<x<3
解析:loga(2+ )-loga(
)-loga( +1)=
+1)=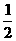
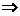 loga
loga =
=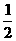 ,a=2.
,a=2.
由g(4)=g(-2)=-5,知g(x)+5=-(x-4)(x+2),故
∴f[g(x)]=log2(-x2+2x+3),由-x2+2x+3>0,得-1<x<3.
9.已知f(x+1)的定义域是[1,2],那么函数f(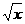 )的定义域为___________________.
)的定义域为___________________.
答案:[4,9]
解析:∵x∈[1,2],∴x+1∈[2,3].
∴f(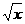 )中的x满足2≤
)中的x满足2≤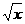 ≤3,即4≤x≤9.
≤3,即4≤x≤9.
8.函数f(x)=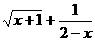 的定义域为_______________.
的定义域为_______________.
答案:[-1,2)∪(2,+∞)
解析:∵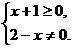 ∴x≥-1且x≠2.
∴x≥-1且x≠2.
7.(2010全国大联,8)已知函数y=f(2x)的定义域是[-1,1],则函数y=f(log2x)的定义域是( )
A.(0,+∞) B.(0,1) C.[1,2] D.[2,4]
答案:D
解析:∵x∈[-1,1],∴2x∈[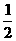 ,2],故log2x∈[
,2],故log2x∈[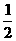 ,2],∴x∈[
,2],∴x∈[ ,4].
,4].
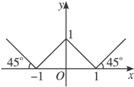
6.已知函数y=f(x)的图象如下图,那么f(x)等于( )
A.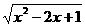 B.
B. C.|x2-1|
D.x2-2|x|+1
C.|x2-1|
D.x2-2|x|+1
答案:B
解析:C、D表示二次函数故首先排除.又∵f(-1)=0,故排除A,故选B.
5.今年有一组实验数据如下:
|
t |
1.998 |
3.002 |
4.001 |
7.995 |
|
S |
1.501 |
2.100 |
3.002 |
4.503 |
把上表反映的数据关系,用一个函数来近似地表达出,其中数据最接近的一个是( )
A.S=1+2t-3
B.S=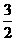 log2t
C.S=
log2t
C.S=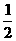 (t2-1)
D.S=-2t+5.5
(t2-1)
D.S=-2t+5.5
答案:B
解析:分别取近似数对(2,1.5),(3,2),(4,3),(8,4.5)代入验证即可选B.
4.设函数f(x)=lgx,g(x)=4x-2x+1-3,则函数f[g(x)]的定义域是( )
A.(-∞,2) B.(2,+∞) C.(log23,+∞) D.(-∞,log23)
答案:C
解析:f[g(x)]=lg[g(x)]=lg(4x-2x+1-3),由4x-2x+1-3>0,得(2x+1)(2x-3)>0,又2x+1>0,
∴2x>3,即x>log23,故选C.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com