
题目列表(包括答案和解析)
9.(2010江西南昌一模,15)定义符号函数sgn x=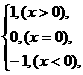 则不等式:x+2>(2x-1)sgn x的解集是____________________________.
则不等式:x+2>(2x-1)sgn x的解集是____________________________.
答案:{x|-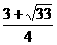 <x<3}
<x<3}
解析:原不等式
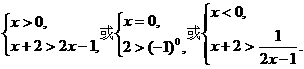
8.设函数f(n)=k(其中n∈N*),k是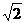 的小数后第n位数,
的小数后第n位数,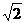 =1.414 213 562 37…,则
=1.414 213 562 37…,则 个的值=______________.
个的值=______________.
答案:1
解析:本题根据题中条件有: =
=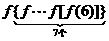 =
=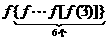 =…=f(2)=1.
=…=f(2)=1.
7.设集合A={1,2,3},B={4,5,6}定义映射f:A→B,使对任意x∈A,都有x2+f(x)+x2f(x)是奇数,则这样的映射f的个数为( )
A.7 B.9 C.10 D.18
答案:B
解析:当x为奇数时,x2+1为偶数,则x2+(x2+1)f(x)为奇数;当x=2时,x2+f(x)+x2f(x)=5f(x)+4为奇数,则f(x)为奇数,即f(2)=5.
∴这样的映射个数为3×3×1=9.
6.如果f(a+b)=f(a)·f(b)且f(1)=2,则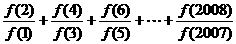 等于( )
等于( )
A.2 007 B.1 003 C.2 008 D.2 006
答案:C
解析:f(a+1)=f(a)·f(1)
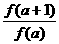 =f(1)=2,原式=2+2+…+2=2×
=f(1)=2,原式=2+2+…+2=2×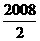 =2 008.
=2 008.
5.如下图所示,①②③三个图象各表示两个变量x、y的对应关系,则有( )
A.都表示映射,且②③表示y关于x的函数
B.②③表示y关于x的函数,且③有反函数
C.都表示y关于x的函数,且②③有反函数
D.都不能表示y关于x的函数

答案:B
解析:根据函数与映射的概念作答知选B.
4.(2010湖北黄冈中学模拟,1)函数y=f(x)的图象与直线x=2的公共点共有( )
A.0个 B.1个 C.0个或1个 D.不能确定
答案:C
解析:如果x=2与函数y=f(x)有公共点,则只有一个公共点,因为自变量取一个值只对应一个函数值.若无交点,则没有公共点,此时的x=2不在y=f(x)的定义域内,故选C.
3.(2010湖北八校模拟,2)设f,g都是由A到A的映射,其对应法则如下表(从上到下):
表1 映射f的对应法则
|
原象 |
1 |
2 |
3 |
4 |
|
象 |
3 |
4 |
2 |
1 |
表2 映射g的对应法则
|
原象 |
1 |
2 |
3 |
4 |
|
象 |
4 |
3 |
1 |
2 |
则与f[g(1)]相同的是( )
A.g[f(1)] B.g[f(2)] C.g[f(3)] D.g[f(4)]
答案:A
解析:f[g(1)]=f(4)=1.g[f(1)]=g(3)=1.
2.下列各组函数中表示同一函数的是( )
A.f(x)=x与g(x)=(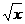 )2
)2
B.f(x)=|x|与g(x)=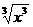
C.f(x)=x|x|与g(x)=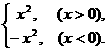
D.f(x)=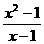 与g(t)=t+1 (t≠1)
与g(t)=t+1 (t≠1)
答案:D
解析:判断的依据是两个函数的定义域和对应法则是否一致.
1.设(x、y)在映射f下的象是(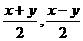 ),则(-5,2)在f的原象是( )
),则(-5,2)在f的原象是( )
A.(-10,4)
B.(-3,-7)
C.(-6,-4) D.(-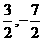 )
)
答案:B
解析: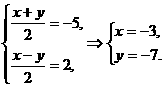
14.已知函数f(x)=lg(x+1),g(x)=2lg(2x+t)(t为参数).
(1)写出函数f(x)的定义域和值域;
(2)当x∈[0,1]时,求函数g(x)解析式中参数t的取值范围;
(3)当x∈[0,1]时,如果f(x)≤g(x),求参数t的取值范围.
解析:(1)函数f(x)的定义域为(-1,+∞),值域为R.
(2)∵2x+t>0,x∈[0,1],∴t>0.
(3)当0≤x≤1时,
f(x)≤g(x)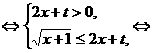 t≥
t≥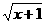 -2x(0≤x≤1)
-2x(0≤x≤1) t≥(
t≥(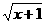 -2x)max.
-2x)max.
设U= 2x,m=
2x,m=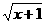 ,则1≤m≤
,则1≤m≤ ,x=m2-1,
,x=m2-1,
∴U=m-2(m2-1)=-2m2+m+2=-2(m-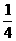 )2+
)2+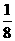 +2.
+2.
∴当m=1(x=0)时,Umax=1.
∴t≥1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com