
题目列表(包括答案和解析)
5.已知真命题:“a≥b是c>d的充分不必要条件”,和“a<b e≤f”那么“c≤d”是“e≤f”的( )
e≤f”那么“c≤d”是“e≤f”的( )
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.?既不充分也不必要条件
答案:A
解析:“a≥b是c>d的充分不必要条件”等价于“c≤d a<b且a<b
a<b且a<b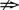 c≤d”,即c≤d
c≤d”,即c≤d e≤f但e≤f
e≤f但e≤f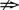 c≤d,故选A.
c≤d,故选A.
4.已知条件p:|x|=x,条件q:x2≥-x,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.?既不充分也不必要条件
答案:A
解析:p:A={0,1},q:B={x|x≤-1或x≥0}.
∵A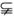 B,∴p是q的充分不必要条件.
B,∴p是q的充分不必要条件.
3.(2010北京西城区一模,5)设a、b∈R,则“a>b”是“a>|b|”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既不是充分条件也不是必要条件
答案:B
解析:a>b并不能得到a>|b|.
如2>-5,但2<|-5|,且a>|b| a>b.故选B.
a>b.故选B.
2.(2010浙江杭州二中模拟,4)“a>2且b>2”是“a+b>4且ab>4”的( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既不充分也不必要条件
答案:A
解析:充分性显然,当a=5,b=1时,有a+b>4,ab>4,但“a>2且b>2”不成立.
1.已知A和B是两个命题,如果A是B的充分但不必要条件,那么 A是
A是 B的( )
B的( )
A.充分但不必要条件 B.必要但不充分条件
C.充要条件 D.既不充分也不必要条件
答案:B
解析:“A B”
B” “
“ B
B
 A”,“B
A”,“B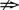 A”等价于“
A”等价于“ A
A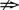
 B”.
B”.
13.△ABC中,|AB|=4,|AC|=2,P、Q分别是AB、AC上的动点,且满足S△APQ=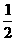 S△ABC,若|AP|=x,|AQ|=y,
S△ABC,若|AP|=x,|AQ|=y,
(1)写出x的取值范围;
(2)求f(x)的解析式.
解析:(1)由S△APQ=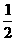 S△ABC
S△ABC
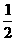 xysinA=
xysinA=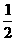 ×
×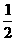 ×2×4sinA
×2×4sinA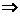 xy=4,而|AB|=4,|AC|=2,
xy=4,而|AB|=4,|AC|=2,
∴0<x≤4,0<y≤2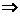 xy≤2x.
xy≤2x.
∴2x≥4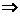 x∈[2,4],
x∈[2,4],
(2)f(x)=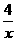 (2≤x≤4).
(2≤x≤4).
12.(2010全国大联考,18)若对任意正实数x,y总有f(xy)=f(x)+f(y):
(1)求f(1);
(2)证明f(x2)=2f(x)和f(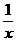 )=-f(x).
)=-f(x).
(1)解析:令y=1,f(x·1)=f(x)+f(1),
∴f(1)=0.
(2)证明:①令y=x,f(x·x)=f(x)+f(x),
∴f(x2)=2f(x).
②令y=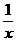 ,f(x·
,f(x·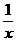 )=f(x)+f(
)=f(x)+f(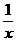 ),
),
∵f(1)=0,
∴有f(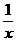 )=-f(x).
)=-f(x).
11.设A=R,B=R,f:x→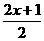 是A→B的映射:
是A→B的映射:
(1)设a∈A,则a在B中的象是什么?
(2)设t∈A,那么t+1在B中的象是什么?
(3)设s∈A,若s→1在映射f下的象为5,则s应是多少?s在映射f下的象是什么?
解析:(1)∵a∈A,而f:x→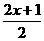 是A→B的映射
是A→B的映射
∴a在B中的象为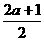 ,
,
即f:a→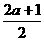 .
.
(2)∵t∈A,A=R,
∴t+1∈A,说明t+1是集合A中的元素.根据映射的定义,元素t+1在B中必定有且只有一个元素与它相对应,故满足对应法则f:x→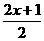 ,元素t+1在B中的象为
,元素t+1在B中的象为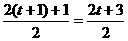 .
.
(3)∵s∈A,
∴s-1∈A,即s-1是集合A中的元素,且有f:s-1→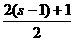 ,又s-1在集合B中的象为5,
,又s-1在集合B中的象为5,
∴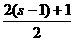 =5,解得s=
=5,解得s=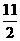 .同理可得s在映射f下在集合B中的象是6.
.同理可得s在映射f下在集合B中的象是6.
10.已知函数f(x)= 若f[f(x0)]=2,则x0=___________________.
若f[f(x0)]=2,则x0=___________________.
答案: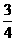 π
π
解析:∵f(-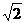 )=(-
)=(-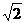 )2=2,
)2=2,
∴f(x0)=-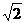 ,又f(
,又f(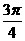 )=2cos
)=2cos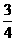 π=-
π=-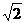 ,
,
∴x0=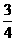 π.
π.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com