13.已知集合A={x|x²-6x+8<0},B={x|(x-a)(x-3a)<0}.

(1)若A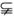B,求a的取值范围；

(2)若A∩B=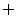,求a的取值范围；

(3)若A∩B={x|3<x<4},求a的取值范围.

解析：A={x|2<x<4},

当a>0时，B={x|a<x<3a};

当a=0时，B=;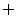

当a<0时，B={x|3a<x<a}.

(1)若A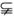B，则a>0且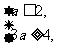

即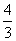≤a≤2.

(2)若A∩B=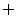，则a≤0满足;

当a>0时，则3a≤2或a≥4.

∴a的取值范围为a≤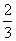或a≥4.

(3)若A∩B={x|3<x<4}，

当a>0时,则a>3；当a≤0时不满足.

∴a的取值范围是a>3.

12.设函数f(x)=log₂(2x-3)的定义域为集合M，函数g(x)=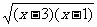的定义域为集合N.

(1)求集合M、N；

(2)求集合M∩N，M∪N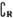，(N)∩M.

解析：(1)由2x-3>0得x>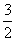,故M={x|x>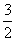},由(x-3)(x-1)>0得x<1或x>3,故N={x|x<1或x>3}.

(2)M∩N={x|x>3}，

M∪N={x|x<1或x>}.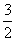

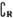∵N={x|1≤x≤3},

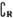∴(N)∩M={x|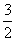<x≤3}.

11.(2010浙江杭州二中模拟，15)已知集合A={x|x²-3x+2=0},集合B={x|x²-ax+a-1=0},若A∪B=A，求实数a的值.

解析：A={x|x²-3x+2=0}={1,2}，

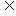A∪B=ABA；

B={x|x²-ax+a-1=0}={x|(x-1)(x-a+1)=0}；

则有a-1=2a=3或a-1=1a=2.

故实数a的值为2或3.

10.已知集合A={-1，2}，B={x|mx+1=0},若A∩B=B，则所有实数m的值组成的集合是_______.

答案：{0，1，-}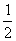

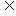解析：A∩B=BBA,

故B为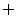或{-1}或{2}.

当B=时，m=0;当B={-1}时，m=1;当B={2}时，m=-.

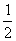9.设全集U={x|0<x<6,x∈N},A={x|x²-5x+q=0},B={x|x²+px+12=0},(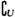A)∪B={1,3,4,5},则集合A=_____________B=_______________.

答案：{2，3}　 {3，4}

解析：U={1，2，3，4，5}，由2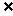{1,3,4,5}知2∈A，∴2²-5×2+q=0即q=6.∴A={2,3},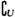A={1,4,5},故3∈B，∴p=-7,B={3,4}.

8.下列各式：①2 006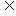{x|x≤2 007};②2 007∈{x|x≤2 007};③{2 007}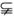{x|x≤2 007};④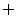∈{x|x<2 007},其中正确的是____________.

答案：②③

解析：①应为2 006∈{x|x≤2 007};④应为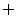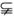{x|x<2 007}.

7.已知向量的集合M={a|a=λ₁(1,0)+(1+λ₁²)(0,1)，λ₁∈R},N={a|a=(1,6)+λ₂(2,4)，λ₂∈R},则M∩N等于(　　 )

A.{(-1，2)}　　　　　　　　　　　　　　　　　 B.{(-1，2)，(3，10)}

C.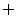　　　　　　　　　　　　　　　　　　　　　 D.{(1,2),(-1,2)}

答案：B

解析：M={a|a=(λ₁,λ₁²+1),λ₁∈R}，N={a|a= (1+2λ₂,6+4λ₂),λ₂∈R},

设a∈M∩N,则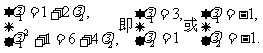故a=(3，10)或(-1，2).

6.设集合M={x|x-m<0},N={y|y=a^x-1,a>0且a≠1,x∈R},若M∩N=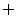，则m的范围是(　　 )

A.m≥-1　　　　　　　 B.m>-1　　　　　　　　　　 C.m≤-1　　　　　　　　 D.m<-1

答案：C

解析：M={x|x<m},N={y|y>-1}，又M∩N=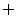，则m≤-1.

5.设M={0，1}，N={11-a,lga,2^a,a},若M∩N={1}，则a值(　　 )

A.存在，且有两个值　　　　　　　　　　　　　　 B.存在，但只有一个值

C.不存在　　　　　　　　　　　　　　　　　　　 D.无法确定

答案：C

解析：若11-a=1,则a=10,lga=1,与集合元素互异性矛盾，同理知lga≠1;若2^a=1,则a=0,此时lga无意义；若a=1,则lga=0,此时M∩N={0，1}.故不存在这样的a值.

4.给定集合A、B，定义一种新运算：A*B={x|x∈A或x∈B,但x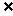A∩B},又已知A={0，1，2}，B={1，2，3}，则A*B等于(　　 )

A.{0}　　　　　　　　　 B.{3}　　　　　　　　　 C.{0，3}　　　　　 D.{0，1，2，3}

答案：C

解析：依题意x∈A∪B,但x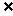A∩B,而A∪B={0，1，2，3}，A∩B={1，2}故A*B={0，3}.