
题目列表(包括答案和解析)
5.已知数列{an}中,a3=2,a7=1,又数列{ }是等差数列,则a11等于( )
}是等差数列,则a11等于( )
A.0
B. C.
C. D.-1
D.-1
[答案]B
[解析]∵ +(7-3)d,
+(7-3)d,
∴d= .
.
∴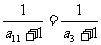 +(11-3)d=
+(11-3)d= ,
,
a11= .
.
4.等差数列{an}的公差为d,前n项的和为Sn,当首项a1和d变化时,a2+a8+a11是一个定值,则下列各数中也为定值的是( )
A.S7 B.S8 C.S13 D.S15
[答案]C
[解析]因a2+a8+a11=3a7,故a7为定值.
又S13= =13a7,
=13a7,
∴选C.
3.等差数列{an}中,若a1+a4+a7=39,a3+a6+a9=27,则前9项的和S9等于( )
A.66 B.99 C.144 D.297
[答案]B
[解析]a1+a4+a7=39 a4=13,a3+a6+a9=27
a4=13,a3+a6+a9=27 a6=9,
a6=9,
S9= =99.
=99.
2.给出下列等式:(ⅰ)an+1-an=p(p为常数);(ⅱ)2an+1=an+an+2(n∈N*);(ⅲ)an=kn+b(k,b为常数)则无穷数列{an}为等差数列的充要条件是( )
A.(ⅰ) B.(ⅰ)(ⅲ)
C.(ⅰ)(ⅱ) D.(ⅰ)(ⅱ)(ⅲ)
[答案]D
[解析]易知三个都是,另外还有一个常见的是{an}的前n项和Sn=an2+bn,(a,b为常数).
1.等差数列{an}前四项和为40,末四项和为72,所有项和为140,则该数列共有( )
A.9项 B.12项 C.10项 D.13项
[答案]C
[解析]∵a1+a2+a3+a4=40,
an+an-1+an-2+an-3=72.
∴a1+an=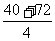 =28.
=28.
又 =140,
=140,
故n=10.
14.(2010湖北黄冈中学模拟,22) 已知函数f(x)= ,x∈(0,+∞),数列{xn}满足xn+1=f(xn),(n=1,2,…),且x1=1.
,x∈(0,+∞),数列{xn}满足xn+1=f(xn),(n=1,2,…),且x1=1.
(1)设an=|xn-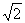 |,证明:an+1<an;
|,证明:an+1<an;
(2)设(1)中的数列{an}的前n项和为Sn,证明:Sn< .
.
证明:(1)an+1=|xn+1-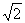 |=|f(xn)-
|=|f(xn)-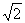 |=
|= .
.
∵xn>0,
∴an+1<(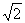 -1)|xn-
-1)|xn-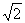 |<|xn-
|<|xn-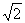 |=an,
|=an,
故an+1<an.
(2)由(1)的证明过程可知
an+1<(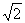 -1)|xn-
-1)|xn-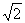 |
|
<(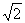 -1)2|xn-1-
-1)2|xn-1-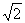 |
|
<…<(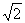 -1)n|x1-
-1)n|x1-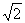 |=(
|=(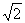 -1)n+1
-1)n+1
∴Sn=a1+a2+…+an<|x1-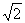 |+(
|+(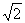 -1)2+…+(
-1)2+…+(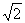 -1)n
-1)n
=(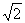 -1)+(
-1)+(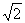 -1)2+…+(
-1)2+…+(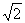 -1)n
-1)n
= [1-(
[1-(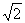 -1)n]<
-1)n]< .
.
13.在等比数列{an}中,a1+a3=10,a2+a4=20,设cn=11-log2a2n.
(1)求数列{cn}的前n项和Sn.
(2)是否存在n∈N*,使得 成立?请说明理由.
成立?请说明理由.
[解析](1)由已知得

∴an=a1qn-1=2n.
∴cn=11-log2a2n=11-log222n
=11-2n.
Sn=c1+c2+…+cn= =-n2+10n.
=-n2+10n.
(2)假设存在n∈N*,使得 即
即 .
.
∴22n+3×2n-3<0,解得 .
.
∵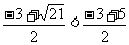 =1,而2n≥2,
=1,而2n≥2,
故不存在n∈N*满足 .
.
12.已知数列{an}:a1,a2,a3,…,an,…,构造一个新数列:a1,(a2-a1),(a3-a2),…,(an-an-1),…此数列是首项为1,公比为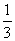 的等比数列.
的等比数列.
(1)求数列{an}的通项;
(2)求数列{an}的前n项和Sn.
[解析](1)由已知得an-an-1=(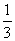 )n-1(n≥2),a=1,
)n-1(n≥2),a=1,
an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)
=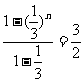 [1-(
[1-(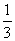 )n].
)n].
(2)Sn=a1+a2+a3+…+an
=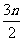 -
- [
[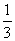 +(
+(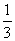 )2+…+(
)2+…+(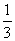 )n]
)n]
=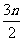 -
- [1-(
[1-(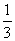 )n]
)n]
=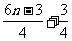 ×(
×(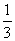 )n.
)n.
11.等比数列{an}的公比为q,作数列{bn}使bn=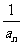 ,
,
(1)求证数列{bn}也是等比数列;
(2)已知q>1,a1= ,问n为何值时,数列{an}的前n项和Sn大于数列{bn}的前n项和Sn′.
,问n为何值时,数列{an}的前n项和Sn大于数列{bn}的前n项和Sn′.
(1)证明:∵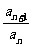 =q,
=q,
∴ 为常数,则{bn}是等比数列.
为常数,则{bn}是等比数列.
(2)[解析]Sn=a1+a2+…+an
= ,
,
Sn′=b1+b2+…+bn
= ,
,
当Sn>Sn′时,
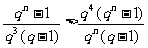 .
.
又q>1,则q-1>0,qn-1>0,
∴ ,即qn>q7,
,即qn>q7,
∴n>7,即n>7(n∈N*)时,Sn>Sn′.
10.给出下列五个命题,其中不正确的命题的序号是_______________.
①若a,b,c成等比数列,则b= ②若a,b,c成等比数列,则ma,mb,mc(m为常数)也成等比数列 ③若{an}的通项an=c(b-1)bn-1(bc≠0且b≠1),则{an}是等比数列 ④若{an}的前n项和Sn=apn(a,p均为非零常数),则{an}是等比数列 ⑤若{an}是等比数列,则an,a2n,a3n也是等比数列
②若a,b,c成等比数列,则ma,mb,mc(m为常数)也成等比数列 ③若{an}的通项an=c(b-1)bn-1(bc≠0且b≠1),则{an}是等比数列 ④若{an}的前n项和Sn=apn(a,p均为非零常数),则{an}是等比数列 ⑤若{an}是等比数列,则an,a2n,a3n也是等比数列
[答案]②④
[解析]②中m=0,ma,mb,mc不成等比数列;
④中a1=ap,a2=ap(p-1),a3=ap2(p-1),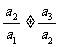 ,故②④不正确,①③⑤均可用定义法判断正确.
,故②④不正确,①③⑤均可用定义法判断正确.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com