
题目列表(包括答案和解析)
7.长城是世界文化遗产,是中华民族的骄傲.某同学家门前的高速公路直达长城(这段公路笔直).星期天,他决定骑自行车前往旅行,他先前进了a千米,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,休息一会儿后,就沿原路返回,走了b千米(b<a)后,记起“不到长城非好汉”这句诗词,就咬咬牙,掉转车头继续前进,则该同学离起点的距离s与时间t的关系示意图是( )
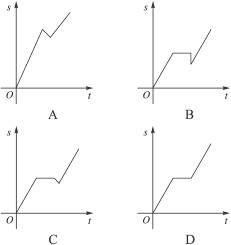
答案:C
解析:由题意知,位移s是时间t的函数,返回时s应减少(时间在推移),故选C.
6.设f(x)是定义在R上的偶函数且f(x+3)=-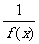 ,又当-3≤x≤-2时,f(x)=2x,则f(113.5)的值是( )
,又当-3≤x≤-2时,f(x)=2x,则f(113.5)的值是( )
A.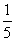 B.-
B.-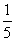 C.
C.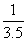 D.-
D.-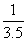
答案:A
解析:因f(x+6)=-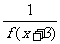 =f(x),故f(x)是以6为周期的函数,f(113.5)=?f(-0.5)=f(0.5)=-
=f(x),故f(x)是以6为周期的函数,f(113.5)=?f(-0.5)=f(0.5)=-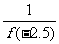 =-
=-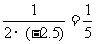 .
.
5.若关于x的方程a2x+(1+lgm)ax+1=0(a>0,且a≠1)有解,则m的取值范围是…( )
A.m>10 B.0<m<100
C.0<m<10 D.0<m≤10-3
答案:D
解析:由方程得lgm=- -1≤-
-1≤-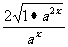 -1=-3.
-1=-3.
于是m≤10-3,注意到对数的定义域,故答案选D.
4.设f(x)对任意x,y∈R有f(x+y)=f(x)+f(y),且当x>0时f(x)<0,则f(x)在区间[a,b]上( )
A.有最大值f(a) B.有最小值f(a)
C.有最大值f(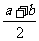 )
D.有最小值f(
)
D.有最小值f(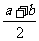 )
)
答案:A
解析:令f(x)=-x,则f(x)在[a,b]递减,排除B、C、D,选A.
3.在一次数学实验中,运用图形计算器采集到如下一组数据:
|
x |
-2.0 |
-1.0 |
0 |
1.00 |
2.00 |
3.00 |
|
y |
0.24 |
0.51 |
1 |
2.02 |
3.98 |
8.02 |
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数)( )
A.y=a+bx B.y=a+bx C.y=a+logbx D.y=a+b/x
答案:A
解析:由x=0可排除C、D.x=0,y=1及x=1,y=2知:若y=a+bx,则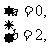 即y=2x,将其他数据代入近似满足;若y=a+bx,则a=1,b=1,即y=1+x,而x=-2时,y=-1不满足.
即y=2x,将其他数据代入近似满足;若y=a+bx,则a=1,b=1,即y=1+x,而x=-2时,y=-1不满足.
2.将进货单价为80元的商品按90元一个售出时,能卖出400个,已知该商品每个涨价1元,其销售量就减少20个,为了赚得最大利润,售价应定为( )
A.每个110元 B.每个105元
C.每个100元 D.每个95元
答案:D
解析:设该商品每个涨价a元,则利润y=(90+a-80)(400-20a)(a=0,1,2,…),即y=20(a+10)(20-a)=-20(a-5)2+4 500,?∴a=5即定价为95元时,y有最大值.
1.一种产品的成本原来为a元,计划在今后m年内使成本平均每年比上一年降低P%,则成本y与经过的年数x的函数关系式为( )
A.y=a(1-P%)x B.y=a(P%)x
C.y=a-(P%)x D.y=a(1+P%)x
答案:A
解析:成本每年比上一年降低P%,即每年成本是上一年的(1-P%)倍.
14.设f(x)=log2x-logx4(0<x<1),数列{an}的通项满足f(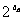 )=2n(n∈N*),问:{an}有没有最小的项?若有求出,若没有请说明理由.
)=2n(n∈N*),问:{an}有没有最小的项?若有求出,若没有请说明理由.
[解析]∵f(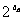 )=log2
)=log2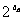 -log
-log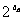 4=2n,
4=2n,
∴an- =2n,
=2n,
即an2-2nan-2=0,
解得:an=n±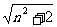 .
.
又∵0<x<1,∴0<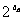 <1,
<1,
∴an<0,故an=n-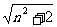 .
.
∴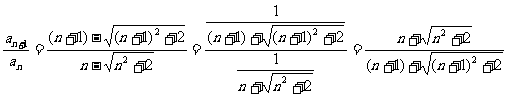 <1.
<1.
而an<0,∴an+1>an,故数列{an}是递增数列,其最小的项是a1=1-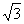 .
.
13.写出满足下列条件的数列的前5项,并归纳出通项公式.
(1)a1=0,an+1=an+(2n-1)(n∈N*);
(2)a1=1,an+1=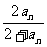 (n∈N*).
(n∈N*).
[解析](1)a1=0,a2=1,a3=4,a4=9,a5=16,an=(n-1)2.
(2)a1=1,a2=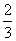 ,a3=
,a3= ,a4=
,a4=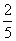 ,a5=
,a5=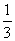 ,an=
,an= .
.
12.已知下面各数列{an}的前n项和Sn的公式,求{an}的通项公式.
(1)Sn=2n2-3n;(2)Sn=3n-2.
[解析](1)当n≥2时,an=Sn-Sn-1=2n2-3n-[2(n-1)2-3(n-1)]=4n-5.
当n=1时,a1=S1=-1满足上式,
∴an=4n-5.
(2)当n≥2时,an=Sn-Sn-1=(3n-2)-(3n-1-2)=2×3n-1,
当n=1时,a1=S1=3-2=1,
∴an=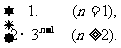
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com