9.函数f(x)= (x²-5x-6)的单调递减区间为________________.

答案：(6，+∞)

解析：∵y=t递减，即求t=x²-5x-6的递增区间且t>0,故f(x)的递减区间为(6，+∞).

8.设方程lg²x+(lg2+lg3)·lgx+lg2·lg3=0的两根为x₁、x₂,那么x₁·x₂的值是________________.

答案：-

解析：lgx₁+lgx₂=-(lg2+lg3)lgx₁x₂=-lg6,x₁·x₂=-.

7.(2010江苏金陵中学模拟，5)设函数f(x)=1-x²+(x-1),则下列说法正确的是(　　 )

A.f(x)是增函数，没有最大值，有最小值

B.f(x)是增函数，没有最大值、最小值

C.f(x)是减函数，有最大值，没有最小值

D.f(x)是减函数，没有最大值、最小值

答案：D

解析：∵x>1，∴y₁=1-x²在(1,+∞)递减.y₂=(x-1)在(1，+∞)上递减，∴f(x)在(1，+∞)上是减函数，且f(x)无最值.

6.当a>1,在同一坐标系中，函数y=a^-x和y=log_ax的图象是(　　 )

答案：A

解析：∵a>1,∴0<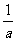<1,故y=a^-x=(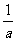)^x单调递减.故选A.

5.(2010北京西城区一模，4)若函数f(x)=则f(log₄3)等于…(　　 )

A.　　　　　　　　 B.3　　　　　　　　 C.　　　　　　　 D.4

答案：B

解析：∵log₄3∈［0，1］.

∴f(x)=4log₄3=3.故选B.

4.若1<a<2,则函数y=log_a(x+2)-1的图象不经过(　　 )

A.第一象限　　　　　　　　　　　　　　 B.第二象限

C.第三象限　　　　　　　　　　　　　　 D.第四象限

答案：D

解析：当x>0时，y=log_a(x+2)-1>log_aa-1=0,故不经过第四象限.

3.函数f(x)=的定义域是(　　 )

A.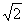［-，-1)∪(1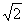，]　　　　　　　　 B.(-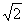，-1)∪(1，)

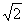C.［-2，1)∪(1，2]　　　　　　　　　　　 D.(-2，-1)∪(1，2)

答案：A

解析：由(x²-1)≥0得0<x²-1≤1,1<x²≤2,

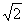∴-≤x<-1或1<x≤.

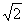2.若2.5^x=1 000,(0.25)^y=1 000,那么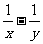等于(　　 )

A.　　　　　　　　 B.　　　　　　　 　C.　　　　　　　　　　 D.

答案：B

解析：2.5^x=1 000x·lg2.5=3,

∴lg2.5.

同理lg0.25.

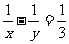∴(lg2.5-lg0.25)=13lg10=.

1.已知log₇［log₃(log₂x)］=0,那么等于(　　 )

A.　　　　　　 B.　　　　　　　 C.　　　　　　　　　 D.

答案：C

解析：log₇［log₃(log₂x)］=0log₃(log₂x)=1,log₂x=3.

∴x=2³=8,.

14.某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场集价与上市时间的关系用图甲中的一条折线表示，西红柿的种植成本与上市时间的关系用乙图中的抛物线段表示.

(1)写出图甲表示的市场售价与时间的函数关系式P=f(t);写出图乙表示的种植成本与时间的函数关系式Q=g(t);

(2)认定市场售价减去种植成本为纯利益，问何时上市的西红柿纯收益最大？

(注：市场售价和种植成本的单位：元/10² kg，时间单位：天)

解析：(1)由题图可得市场售价与时间的函数关系为f(t)=

由题图可得种植成本与时间的函数关系为g(t)=(t-150)²+100,0≤t≤300.

(2)设t时刻的纯收益为h(t),则由题?意得?h(t)=f(t)-g(t),

即h(t)=

当0≤t≤200时，配方整理得

h(t)=-(t-50)²+100,

所以，当t=50时，h(t)在区间［0，200］上取得最大值100;

当200<t≤300时，配方整理得

h(t)=-(t-350)²+100,

所以，当t=300时，

h(t)在区间(200，300］上取得最大值87.5.

综上，由100>87.5可知，h(t)在区间［0，300］上可以取得最大值100，此时t=50,即从二月一日开始的第50天时，上市的西红柿纯收益最大.课时训练15　 函数的综合应用