12．已知函数f(x)＝，则不等式x+(x+2)f(x+2)≤4的解集是(　)

A.　 　　　　　　　　　B.

C.　 　　　　　　　　　　　　D.

解析：当x+2≥0即x≥－2时，不等式x+(x+2)f(x+2)≤4化为：x+(x+2)×1≤4，即x≤1，故－2≤x≤1；当x+2<0即x<－2时，不等式x+(x+2)f(x+2)≤4化为：x+(x+2)×(－1)≤4，即－2≤4，这显然成立．综上可知，原不等式的解集为.

答案：B

11．已知O为直角坐标系原点，P、Q两点的坐标均满足不等式组则tan∠POQ的最大值等于　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　B．1　　　　　 C.　 　　　　　　　D．0

解析：作出可行域，则P、Q在图中所示的位置时，∠POQ最大，即tan∠POQ最大，

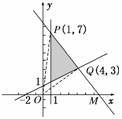∠POQ＝∠POM－∠QOM，

tan∠POQ＝tan(∠POM－∠QOM)＝

＝＝1，所以最大值为1.

答案：B

10．函数y＝log_a(x+3)－1(a>0，a≠1)的图象恒过定点A，若A在直线mx+ny+1＝0上，其中m、n均为正数，则+的最小值为　　　　　　　　　　　　　　 (　)

A．2　 　　　　　B．4 　　　　　　C．6　 　　　　　　　D．8

解析：函数y＝log_a(x+3)－1的图象恒过定点A(－2，－1)，∴－2m－n+1＝0，即2m+n＝1，令u＝+＝(+)·(2m+n)＝4++≥8.

答案：D

9．p＝+，q＝·(m、n、a、b、c、d均为正数)，则p、q的大小为　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　(　)

A．p≥q　　　　　 　B．p≤q　　　　 C．p＞q 　　　　　D．不确定

解析：q＝ ≥

＝+＝p.

答案：B

8．若平面区域是一个三角形，则k的取值范围是　　　　　　　 (　)

A．(0,2] 　　　　　　　　　　B．(－∞，－2]∪　 　　　　　　D．

解析：如图，只有直线y＝kx－2与线段AB相交(不包括点A)

或与线段CD相交(不包括点D)，可行域才能构成三角形，

故k∈．

答案：C

7．(2010·泉州模拟)设x，y是关于m的方程m²－2am+a+6＝0的两个实根，则(x－1)²+(y－1)²的最小值是　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－12　 　　　　B．18　　　　 C．8 　　　　D.

解析：∵x+y＝2a，xy＝a+6，

∴(x－1)²+(y－1)²＝x²+y²－2(x+y)+2

＝(x+y)²－2(x+y)－2xy+2

＝4a²－4a－2(a+6)+2

＝4a²－6a－10

＝4(a－)²－.

又∵x、y是方程m²－2am+a+6＝0的两根，

∴Δ＝4a²－4(a+6)≥0，即a≥3或a≤－2.

∴当a＝3时，(x－1)²+(y－1)²的最小值为8.

答案：C

6．已知不等式ax²+bx+c>0的解集为，则不等式cx²+bx+a<0的解集为(　)

A.　 　　　　　　　　　　　　B.

C.　　　　　　　　　　 　D.

解析：由题意⇒

∴cx²+bx+a<0可化为x²+x+>0，即x²－x+>0，解得.

答案：D

5．设a，b∈R，则“a+b＝1”是“4ab≤1”的　　　　　　　　　　　　　 (　)

A．充分不必要条件　　　　　　 　B．必要不充分条件

C．充要条件 　　　　　　　　　　D．既不充分也不必要条件

解析：若“a+b＝1”，则4ab＝4a(1－a)＝－4(a－)²+1≤1；若“4ab≤1”，取a＝－4，b＝1，a+b＝－3，即“a+b＝1”不成立；则“a+b＝1”是“4ab≤1”的充分不必要条件．

答案：A

4．(2010·诸城模拟)若log_mn＝－1，则3n+m的最小值是　　　　　　　　　　 (　)

A．2　 　　　　　　B．2　 　　　　　C．2　 　　　　　　　D.

解析：∵log_mn＝－1，

∴m>0，m≠1，n>0，mn＝1.

∴3n+m≥2＝2

即3n+m的最小值为2.

答案：B

3．根据给出的数塔猜测1 234 567×9+8＝　　　　　　　　　　　　　　　　　 (　)

1×9+2＝11

12×9+3＝111

123×9+4＝1 111

1 234×9+5＝11 111

12 345×9+6＝111 111

A．11 111 110　 　　　　B．11 111 111 　　　　C．11 111 112 　　　　D．11 111 113

解析：数塔的右侧的规律是，逐次加1.

答案：B