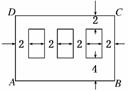
22．(文)(本小题满分14分)如图，某农厂要修建3个矩形养鱼塘，

每个面积为10 000平方米．鱼塘前面要留4米宽的运料通道，

其余各边为2米宽的堤埂，问每个鱼塘的长、宽各为多少米时

占地面积最少？

解：设每个鱼塘的宽为x米，

且x＞0，且AB＝3x+8，AD＝+6，

则总面积y＝(3x+8)(+6)

＝30 048++18x

≥30 048+2 ＝32 448，

当且仅当18x＝，即x＝时，等号成立，此时＝150.

即鱼塘的长为150米，宽为米时，占地面积最少为32448平方米．

(理)(本小题满分14分)(2009·安徽高考)首项为正数的数列{a_n}满足a_n+1＝(a+3)，n∈N₊.

(1)证明：若a₁为奇数，则对一切n≥2，a_n都是奇数；

(2)若对一切n∈N₊都有a_n+1>a_n，求a₁的取值范围．

解：(1)证明：已知a₁是奇数，假设a_k＝2m－1是奇数，其中m为正整数，则由递推关系得a_k+1＝＝m(m－1)+1是奇数．

根据数学归纳法，对任何n≥2，a_n都是奇数．

(2)法一：由a_n+1－a_n＝(a_n－1)(a_n－3)知，a_n+1>a_n当且仅当a_n<1或a_n>3.

另一方面，若0<a_k<1，则0<a_k+1<＝1；

若a_k>3，则a_k+1>＝3.

根据数学归纳法得，0<a₁<1⇔0<a_n<1，∀n∈N₊；

a₁>3⇔a_n>3，∀n∈N₊.

综上所述，对一切n∈N₊都有a_n+1>a_n的充要条件是0<a₁<1或a₁>3.

法二：由a₂＝>a₁，得a－4a₁+3>0，

于是0<a₁<1或a₁>3.

a_n+1－a_n＝－＝，

因为a₁>0，a_n+1＝，所以所有的a_n均大于0，

因此a_n+1－a_n与a_n－a_n－1同号．

根据数学归纳法，∀n∈N₊，a_n+1－a_n与a₂－a₁同号．

因此，对一切n∈N₊都有a_n+1>a_n的充要条件是0<a₁<1或a₁>3.

21．(本小题满分12分)某工厂生产甲、乙两种产品，计划每天每种产品的生产量不少于15吨，已知生产甲产品1吨，需煤9吨，电力4千瓦时，劳力3个；生产乙产品1吨，需煤4吨，电力5千瓦时，劳力10个；甲产品每吨的利润为7万元，乙产品每吨的利润为12万元；但每天用煤不超过300吨，电力不超过200千瓦时，劳力只有300个．问每天生产甲、乙两种产品各多少吨，才能使利润总额达到最大？

解：设每天生产甲、乙两种产品分别为x吨、y吨，利润总额为z万元，

则线性约束条件为

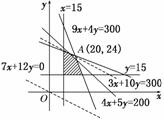目标函数为z＝7x+12y，

作出可行域如图，

作出一组平行直线7x+12y＝t，

当直线经过直线4x+5y＝200和直线3x+10y＝300的交点A(20,24)时，利润最大．

即生产甲、乙两种产品分别为20吨、24吨时，利润总额最大，z_max＝7×20+12×24＝428(万元).

20．(本小题满分12分)解关于x的不等式(1－ax)²<1.

解：由(1－ax)²<1得

a²x²－2ax+1<1，即ax(ax－2)<0.

(1)当a＝0时，不等式转化为0<0，故x无解．

(2)当a<0时，不等式转化为x(ax－2)>0，

即x(x－)<0.

∵<0，∴不等式的解集为.

(3)当a>0时，不等式转化为x(ax－2)<0，

又>0，∴不等式的解集为.

综上所述：当a＝0时，不等式解集为空集；

当a<0时，不等式解集为；

当a>0时，不等式解集为.

19．(本小题满分12分)已知函数f(x)＝ax²+4(a为非零实数)，设函数F(x)＝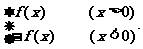

(1)若f(－2)＝0，求F(x)的表达式；

(2)mn<0，m+n>0，试判断F(m)+F(n)能否大于0?

解：(1)由f(－2)＝0,4a+4＝0⇒a＝－1，

∴F(x)＝ (2)∵，

∴m，n一正一负．

不妨设m>0且n<0，则m>－n>0，

F(m)+F(n)＝f(m)－f(n)＝am²+4－(an²+4)

＝a(m²－n²)，

当a>0时，F(m)+F(n)能大于0，

当a<0时，F(m)+F(n)不能大于0.

18．(本小题满分12分)解下列问题：

(1)已知a＞0，b＞0，且4a+b＝1，求ab的最大值；

(2)已知x＞2，求x+的最小值；

(3)已知x＞0，y＞0，且x+y＝1，求+的最小值．

解：(1)法一：∵a＞0，b＞0,4a+b＝1，

∴1＝4a+b≥2＝4，

当且仅当4a＝b＝，即a＝，b＝时，等号成立．

∴≤，∴ab≤.所以ab的最大值为.

法二：∵a＞0，b＞0,4a+b＝1，

∴ab＝4a·b≤()²＝，

当且仅当4a＝b＝，即a＝，b＝时，等号成立．

所以ab的最大值为.

(2)∵x＞2，∴x－2＞0，

∴x+＝x－2++2

≥2 +2＝6，

当且仅当x－2＝，即x＝4时，等号成立．

所以x+的最小值为6.

(3)∵x＞0，y＞0，x+y＝1，

∴+＝(x+y)(+)＝13++

≥13+2＝25，

当且仅当＝时等号成立，由得

∴当x＝，y＝时取等号．

所以+的最小值为25.

17．(本小题满分12分)设x＜y＜0，试比较(x²+y²)(x－y)与(x²－y²)·(x+y)的大小．

解：(x²+y²)(x－y)－(x²－y²)(x+y)

＝(x－y)

＝－2xy(x－y)，

∵x＜y＜0，∴xy＞0，x－y＜0，∴－2xy(x－y)＞0，

∴(x²+y²)(x－y)＞(x²－y²)(x+y)．

16．(2010·宜昌模拟)若实数x，y满足且z＝2x+y的最小值为3，则实　　 数b的值为________．

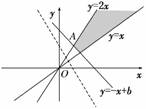解析：由约束条件作出可行域(如图)，

当平行直线系y＝－2x+z经过可行域内的点A(，)时，z取得最小值，即2×+＝3，解之得b＝.

答案：

15．设x>0，则y＝3－2x－的最大值等于________．

解析：∵x>0，则2x+≥2，所以－(2x+)≤－2，2x＝时，x＝时等号成立，则y＝3－2x－≤3－2，即y_max＝3－2.

答案：3－2

14．对于平面几何中的命题：“夹在两条平行线这间的平行线段相等”，在立体几何中，类比上述命题，可以得到命题：“__________________”，这个类比命题的真假性是________．

解析：由类比推理可知．

答案：夹在两个平行平面间的平行线段相等　真命题

13．观察下列不等式：1＞，1++＞1,1+++…+＞，1+++…+＞2,1+++…+＞，…，由此猜测第n个不等式为________(n∈N^*)．

解析：3＝2²－1,7＝2³－1,15＝2⁴－1，可猜测：1+++…+＞(n∈N^*)．

答案：1+++…+＞