12．(2010·南通模拟)已知函数f(x)＝x³+ax²+bx+c在x＝－与x＝1时都取得极值，

(1)求a，b的值与函数f(x)的单调区间；

(2)若对x∈，不等式f(x)＜c²恒成立，求c的取值范围．

解：(1)f(x)＝x³+ax²+bx+c，f′(x)＝3x²+2ax+b，

由f′(－)＝－a+b＝0，f′(1)＝3+2a+b＝0得a＝－，b＝－2，

f′(x)＝3x²－x－2＝(3x+2)(x－1)，函数f(x)的单调区间如下表：

x	(－∞，－)	－	(－，1)	1	(1，+∞)
f′(x)	+	0	－	0	+
f(x)	?	极大值	?	极小值	?

所以函数f(x)的递增区间是(－∞，－)与(1，+∞)，递减区间(－，1)；

(2)f(x)＝x³－x²－2x+c，x∈，当x＝－时，f(－)＝+c为极大值，而f(2)＝2+c，则f(2)＝2+c为最大值，要使f(x)＜c²，x∈恒成立，则只需要c²＞f(2)＝2+c，得c＜－1，或c＞2.

11．设f′(x)是函数f(x)的导函数，将y＝f(x)和y＝f′(x)的图象画在同一个直角坐标系中，不可能正确的是　　　　　　　　　　　　　　　　 　　　　　　　　(　)

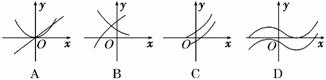
解析：对于图A来说，抛物线为函数f(x)，直线为f′(x)；对于图B来说，上凸的曲线为函数f(x)，下凹的曲线为f′(x)；对于图C来说，下面的曲线为函数f(x)，上面的曲线f′(x)．只有图D不符合题设条件．

答案：D

10．某公司生产某种产品，固定成本为20 000元，每生产一单位产品，成本增加100

元，已知总营业收入R与年产量x的关系是R＝R(x)＝

，则总利润最大时，每年生产的产品是　　　 (　)

A．100　 　　B．150　　　 C．200 　　　　D．300

解析：由题意得，总成本函数为C＝C(x)＝20 000+100x，

所以总利润函数为

P＝P(x)＝R(x)－C(x)

＝

而P′(x)＝

令P′(x)＝0，得x＝300，易知x＝300时，P最大．

答案：D

9.已知对任意实数x，都有f(－x)＝－f(x)，g(－x)＝g(x)，且x>0时， f′(x)>0，g′(x)>0，则x<0时　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　(　)

A．f′(x)>0，g′(x)>0 　　　　　　　B．f′(x)>0，g′(x)<0

C．f′(x)<0，g′(x)>0　 　　　　　　D．f′(x)<0，g′(x)<0

解析：由题意知f(x)是奇函数，g(x)是偶函数．当x＞0时，f(x)，g(x)都单调递增，则当x＜0时，f(x)单调递增，g(x)单调递减，即f′(x)＞0，g′(x)＜0.

答案：B

8．(文)已知函数f(x)＝x³+ax²+bx+c，曲线y＝f(x)在点x＝1处的切线l不过第四象限且斜率为3，又坐标原点到切线l的距离为，若x＝时，y＝f(x)有极值，

(1)求a，b，c的值；

(2)求y＝f(x)在上的最大值和最小值．

解：(1)由f(x)＝x³+ax²+bx+c，得

f′(x)＝3x²+2ax+b.

当x＝1时，切线l的斜率为3，可得2a+b＝0.　　　　　　　　　　　　　　　　 ①

当x＝时，y＝f(x)有极值，则f′()＝0，可得

4a+3b+4＝0.　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　②

由①②解得a＝2，b＝－4.

设切线l的方程为y＝3x+m.

由原点到切线l的距离为，则＝，

解得m＝±1.

∵切线l不过第四象限，∴m＝1.

由于切点的横坐标为x＝1，∴f(1)＝4.

∴1+a+b+c＝4，∴c＝5；

(2)由(1)可得f(x)＝x³+2x²－4x+5，

∴f′(x)＝3x²+4x－4.

　令f′(x)＝0，得x＝－2，x＝.

f(x)和f′(x)的变化情况如下表：

x	[－3，－2)	－2	(－2，)		(，1]
f′(x)	+	0	－	0	+
f(x)	?	极大值	?	极小值	?

∴f(x)在x＝－2处取得极大值f(－2)＝13，

在x＝处取得极小值f()＝.

又f(－3)＝8，f(1)＝4，

∴f(x)在上的最大值为13，最小值为.

(理)已知函数f(x)＝x³+2bx²+cx－2的图象在与x轴交点处的切线方程是y＝5x－10.

(1)求函数f(x)的解析式；

(2)设函数g(x)＝f(x)+mx，若g(x)的极值存在，求实数m的取值范围以及函数g(x)取得极值时对应的自变量x的值．

解：(1)由已知，切点为(2,0)，故有f(2)＝0，

即4b+c+3＝0.　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

f′(x)＝3x²+4bx+c，由已知，f′(2)＝12+8b+c＝5.

得8b+c+7＝0.　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ②

联立①、②，解得c＝1，b＝－1，

于是函数解析式为f(x)＝x³－2x²+x－2.

(2)g(x)＝x³－2x²+x－2+mx，

g′(x)＝3x²－4x+1+，令g′(x)＝0.

当函数有极值时，Δ≥0，方程3x²－4x+1+＝0有实根，

由Δ＝4(1－m)≥0，得m≤1.

①当m＝1时，g′(x)＝0有实根x＝，在x＝左右两侧均有g′(x)＞0，故函数g(x)无极值．

②当m＜1时，g′(x)＝0有两个实根，

x₁＝(2－)，x₂＝(2+)，

当x变化时，g′(x)、g(x)的变化情况如下表：

x	(－∞，x1)	x1	(x1，x2)	x2	(x2，+∞)
g′(x)	+	0	－	0	+
g(x)	?	极大值	?	极小值	?

故在m∈(－∞，1)时，函数g(x)有极值；

当x＝(2－)时g(x)有极大值；

当x＝(2+)时g(x)有极小值．

7．函数y＝sin2x－x，x∈的最大值是________，最小值是________．

解析：∵y′＝2cos2x－1＝0，∴x＝±.

而f(－)＝－+，f()＝－，

端点f(－)＝，f()＝－，

所以y的最大值是，最小值是－.

答案：　－

2.若函数h(x)＝2x－+在(1，+∞)上是增函数，则实数k的取值范围是　　　 (　)

A． 　　　D．(－∞，2]

解析：因为h′(x)＝2+，所以h′(x)＝2+＝≥0在(1，+∞)上恒成立，即k≥－2x²在(1，+∞)上恒成立，所以k∈　　　 C．(－∞，－1)　 　　　D．(1，+∞)

解析：由f′(x)＝3x²－3＝3(x－1)(x+1)，

且当x＜－1时，f′(x)＞0；

当－1＜x＜1时，f′(x)＜0；当x＞1时，f′(x)＞0.

所以当x＝－1时函数f(x)有极大值，当x＝1时函数f(x)有极小值．

要使函数f(x)有3个不同的零点，只需满足

解之得－2＜a＜2.

答案：A

1.(2009·广东高考)函数f(x)＝(x－3)e^x的单调递增区间是说明　　　　　　　　　 (　)

A．(－∞，2)　 　　B．(0,3)　　 C．(1,4) 　　D．(2，+∞)

解析：f(x)＝(x－3)·e^x，f′(x)＝e^x(x－2)＞0，

∴x＞2.

∴f(x)的单调递增区间为(2，+∞)．

答案：D

12．(2010·株州模拟)已知二次函数f(x)＝ax²+bx+c(x∈R)，满足f(0)＝f()＝0，且f(x)的最小值是－.设数列{a_n}的前n项和为S_n，对一切n∈N^*，点(n，S_n)在函数f(x)的图象上．

(1)求数列{a_n}的通项公式；

(2)通过b_n＝构造一个新的数列{b_n}，是否存在非零常数c，使得{b_n}为等差数列；

(3)令c_n＝，设数列{c_n·2c_n}的前n项和为T_n，求T_n.

解：(1)因为f(0)＝f()＝0，所以f(x)的对称轴为x＝＝，又因为f(x)的最小值是－，由二次函数图象的对称性可设f(x)＝a(x－)²－.

又f(0)＝0，所以a＝2，所以f(x)＝2(x－)²－＝2x²－x.

因为点(n，S_n)在函数f(x)的图象上，所以S_n＝2n²－n.当n＝1时，a₁＝S₁＝1；当n≥2时，a_n＝S_n－S_n－1＝4n－3(n＝1时也成立)，所以a_n＝4n－3(n∈N^*)．

(2)因为b_n＝＝＝，令c＝－(c≠0)，即得b_n＝2n，此时数列{b_n}为等差数列，所以存在非零常数c＝－，使得{b_n}为等差数列．

(3)c_n＝＝＝2n，则c_n·2c_n＝2n×2²ⁿ＝n×2²ⁿ⁺¹.

所以T_n＝1×2³+2×2⁵+…+(n－1)2^2n－1+n×2²ⁿ⁺¹，

4T_n＝1×2⁵+2×2⁷+…+(n－1)2²ⁿ⁺¹+n×2²ⁿ⁺³，

两式相减得：－3T_n＝2³+2⁵+…+2²ⁿ⁺¹－n×2²ⁿ⁺³＝－n·2²ⁿ⁺³，

T_n＝+＝.

11．(文)在等差数列{a_n}中，若a₁<0，S₉＝S₁₂，则当n等于________时，S_n取得最小值．

解析：设数列{a_n}的公差为d，则由题意得

9a₁+×9×(9－1)d＝12a₁+×12×(12－1)d，

即3a₁＝－30d，∴a₁＝－10d.

∵a₁<0，∴d>0.

∴S_n＝na₁+n(n－1)d＝dn²－dn

＝²－.

∴S_n有最小值，又n∈N^*，

∴n＝10，或n＝11时，S_n取最小值．

答案：10或11

(理)若数列{a_n}是等差数列，数列{b_n}满足b_n＝a_n·a_n+1·a_n+2(n∈N^*)，{b_n}的前n项和用S_n表示，若{a_n}满足3a₅＝8a₁₂＞0，则当n等于________时，S_n取得最大值．

解析：(先判断数列{a_n}中正的项与负的项)

∵3a₅＝8a₁₂＞0，∴3a₅＝8(a₅+7d)＞0，

解得a₅＝－d＞0，∴d＜0，∴a₁＝－d，

故{a_n}是首项为正数的递减数列．

由⇒⇒15≤n≤16，

∴n＝16.

答案：16