10.已知P(x，y)是函数y＝e^x+x图象上的点，则点P到直线2x－y－3＝0的最小距离为(　)

A.　　　 　B.　　　 C.　 　　　　　　D.

解析：将直线2x－y－3＝0平移到与函数y＝e^x+x的图象相切时，切点到直线2x－y－　 3＝0的距离最短，故关键是求出切点的坐标.由y′＝e^x+1＝2解得x＝0，代入函数y＝e^x+x易得y＝1，点(0,1)到直线2x－y－3＝0的距离为＝.

答案：D

9.已知f′(x)是函数y＝f(x)的导函数，且y＝f′(x)的图象如图所示，则函数y＝f(x)的图象可能是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

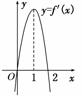
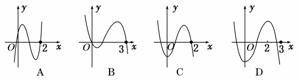
解析：由导函数f′(x)的图象可知，f′(x)在x∈(0,2)上恒大于零，在x∈(2，+∞)上恒小于0，由函数的导数与函数的单调性关系可以知道，函数f(x)在x∈(0,2)上单调递增，在x∈(2，+∞)上单调递减，结合选项可知选D.

答案：D

8.已知<x<，设a＝2^1－sinx，b＝2^cosx，c＝2^tanx，则　　　　　　　　　　　　 (　)

A.a<b<c　　B.b<a<c　　　 C.a<c<b 　　　　D.b<c<a

解析：因为<x<，所以0<cosx<sinx<1<tanx，而sinx+cosx>1，cosx>1－sinx，故a<b<c.

答案：A

7.函数f(x)＝ln(1－x²)的图象只可能是　　　　　　　　　　　　　　　　 (　)

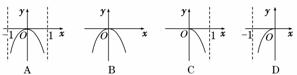
解析：函数f(x)＝ln(1－x²)的定义域为(－1,1)，且f(x)为偶函数，当x∈(0,1)时，函数f(x)＝ln(1－x²)为单调递减函数；当x∈(－1,0)时，函数f(x)为单调递增函数，且函数值都小于零，所以其图象为A.

答案：A

6.曲线y＝x³在点(1,1)处的切线与x轴及直线x＝1所围成的三角形的面积为　　 (　)

A.　 　　　B.　　　　 C.　 　　　　D.

解析：由题可知，曲线y＝x³在点(1,1)处的切线方程为y－1＝3(x－1)，即y＝3x－2，令y＝0，得x＝，画出图形可知，所围成三角形的面积为S＝×(1－)×1＝.

答案：B

5.(文)已知函数f(x)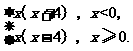＝则函数f(x)的零点个数为 　　　　　　(　)

A.1 　　　B.2 　　　　C.3 　　　　　D.4

解析：当x＜0时，由x(x+4)＝0⇒x＝－4；当x≥0时，由x(x－4)＝0⇒x＝4或x＝0.

答案：C

(理)已知f(x)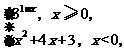＝则方程f(x)＝2的实数根的个数是　　　　 (　)

A.0　 　　　B.1　　　　　 C.2 　　　　　　　D.3

解析：令3^1－x＝2，∴1－x＝log₃2.∴x＝1－log₃2.

又∵log₃2<log₃3＝1，∴x＝1－log₃2>0.

∴这个实根符合题意.

令x²+4x+3＝2，则x²+4x+1＝0.

解得两根x₁＝－2－，x₂＝－2+，

x₁和x₂均小于0，符合题意.

答案：D

4.某学校开展研究性学习活动，一组同学获得了下面的一组实验数据：

现准备用下列四个函数中的一个近似地表示这些数据的规律，其中最接近的一个是(　)

A.y＝2x－2 　　　B.y＝()^x　　　 C.y＝log₂x 　　　　D.y＝(x²－1)

解析：直线是均匀的，故选项A不是；指数函数y＝()^x是单调递减的，也不符合要 求；对数函数y＝log₂x的增长是缓慢的，也不符合要求；将表中数据代入选项D中，基本符合要求.

答案：D

3.设m，n∈R，函数y＝m+log_nx的图象如图所示，则有 (　)

A.m＜0,0＜n＜1　　　 B.m＞0，n＞1

C.m＞0,0＜n＜1　　　 D.m＜0，n＞1

解析：由函数图象可知该函数为增函数，所以n＞1，又图象与x轴的交点在(0,1)之间，故该图象是由y＝log_nx的图象向上平移得到的，所以m＞0.

答案：B

2.函数f(x)＝lnx－的零点所在的区间是　　　　　　　　　　　　　　　　　 (　)

A.(0,1) 　　　B.(1，e)　　 C.(e,3) 　　　　　　　D.(3，+∞)

解析：代入验证可知，只有B中：f(1)·f(e)＝(ln1－)(lne－)＜0，又∵f′(x)＝+＝＞0，故在(1，e)上函数f(x)存在零点.

答案：B

1.已知集合A＝{x|x＜3}，B＝{x|2^x－1＞1}，则A∩B＝　　　　　　　　　　　　 (　)

A.{x|x＞1}　B.{x|x＜3}　　　　 C.{x|1＜x＜3} 　　　　　　D.∅

解析：集合B中不等式2^x－1＞1⇒2^x－1＞2⁰⇒x＞1，所以A∩B＝{x|1＜x＜3}.

答案：C