
题目列表(包括答案和解析)
3.甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面.不同的安排方法共有________种.
解析:分三类:甲在周一,共有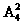 种排法;
种排法;
甲在周二,共有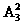 种排法;
种排法;
甲在周三,共有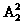 种排法.
种排法.
∴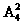 +
+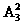 +
+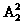 =20.
=20.
答案:20
|
题组二 |
分步乘法计数原理 |
2.某校开设10门课程供学生选修,其中A,B,C三门由于上课时间相同,至多选一门.学校规定,每位同学选修三门,则每位同学不同的选修方案种数是 ( )
A.120 B.98 C.63 D.56
解析:分两类:第一类A,B,C三门课都不选,有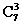 =35种方案;第二类A,B,C中选一门,剩余7门课中选两门,有
=35种方案;第二类A,B,C中选一门,剩余7门课中选两门,有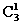
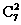 =63种方案.故共有35+63=98种方案.
=63种方案.故共有35+63=98种方案.
答案:B
1.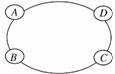 右图是某汽车维修公司的维修点环形分布图,公司在
右图是某汽车维修公司的维修点环形分布图,公司在
年初分配给A、B、C、D四个维修点某种配件各50件.
在使用前发现需将A、B、C、D四个维修点的这批配件
分别调整为40、45、54、61件,但调整只能在相邻维修
点之间进行,那么要完成上述调整,最少的调动件次(n件配件从一个维修点调整到相邻维修点的调动件次为n)为 ( )
A.15 B.16 C.17 D.18
解析:只需A处给D处10件,B处给C处5件,C处给D处1件,共16件次.
答案:B
12.(文)设t≠0,点P(t,0)是函数f(x)=x3+ax与g(x)=bx2+c的图象的一个公共点,两函数的图象在点P处有相同的切线.试用t表示a,b,c.
解:因为函数f(x),g(x)的图象都过点(t,0),
所以f(t)=0,
即t3+at=0.因为t≠0,所以a=-t 2.
g(t)=0,即bt2+c=0,所以c=ab.
又因为f(x),g(x)在点(t,0)处有相同的切线,
所以f′(t)=g′(t).
而f′(x)=3x2+a,g′(x)=2bx,
所以3t2+a=2bt.
将a=-t2代入上式得b=t.因此c=ab=-t3.
故a=-t2,b=t,c=-t3.
(理)已知函数f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12,和直线m:y=kx+9,又f′(-1)=0.
(1)求a的值;
(2)是否存在k的值,使直线m既是曲线y=f(x)的切线,又是曲线y=g(x)的切线?如果存在,求出k的值;如果不存在,请说明理由.
解:(1)f′(x)=3ax2+6x-6a,f′(-1)=0,
即3a-6-6a=0,∴a=-2.
(2)∵直线m恒过定点(0,9),先求直线m是曲线y=g(x)的切线,设切点为(x0,3 +6x0+12),
+6x0+12),
∵g′(x0)=6x0+6,
∴切线方程为y-(3 +6x0+12)=(6x0+6)(x-x0),将点(0,9)代入,得x0=±1,
+6x0+12)=(6x0+6)(x-x0),将点(0,9)代入,得x0=±1,
当x0=-1时,切线方程为y=9;
当x0=1时,切线方程为y=12x+9.
由f′(x)=0得-6x2+6x+12=0,即有x=-1或x=2,
当x=-1时,y=f(x)的切线方程为y=-18;
当x=2时,y=f(x)的切线方程为y=9.
∴公切线是y=9.
又有f′(x)=12得-6x2+6x+12=12,∴x=0或x=1.
当x=0时,y=f(x)的切线方程为y=12x-11;
当x=1时,y=f(x)的切线方程为y=12x-10,
∴公切线不是y=12x+9.
综上所述公切线是y=9,此时存在,k=0.
11.(文)(2010·开原模拟)设a>0,f(x)=a2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为,则点P到曲线y=f(x)对称轴距离的取值范围为( )
A. B. C. D.
解析:∵y=f(x)在点P(x0,f(x0))处切线的倾斜角的范围为,∴0≤f′(x0)≤1,即0≤2ax0+b≤1,∴-≤x0≤,∴0≤x0+≤,即点P到曲线y=f(x)对称轴的距离的取值范围为.
答案:B
(理)曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是 ( )
A. B.2 C.3 D.0
解析:设曲线上过点P(x0,y0)的切线平行于直线2x-y+3=0,此切点到直线2x-y+3=0的距离最短,即斜率是2,则
y′|x=x0=[·(2x-1)′]|x=x0
=|x=x0==2.
解得x0=1,所以y0=0,即点P(1,0),
点P到直线2x-y+3=0的距离为=,
∴曲线y=ln(2x-1)上的点到直线2x-y+3=0的最短距离是.
答案:A
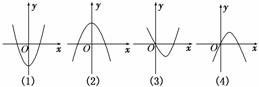
10.下图中,有一个是函数f(x)=x3+ax2+(a2-1)x+1(a∈R,a≠0)的导函数f′(x)的图象,则f(-1)= ( )
A.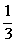 B.-
C.
B.-
C.  D.-或
D.-或
解析:∵f′(x)=x2+2ax+(a2-1),
∴导函数f′(x)的图象开口向上.
又∵a≠0,∴其图象必为第(3)个图.
由图象特征知f′(0)=0,且-a>0,∴a=-1.
故f(-1)=--1+1=-.
答案:B
9.已知函数f(x)=x3+x-16.
(1)求曲线y=f(x)在点(2,-6)处的切线的方程;
(2)直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切点坐标;
(3)如果曲线y=f(x)的某一切线与直线y=-x+3垂直,求切点坐标与切线的方程.
解:(1)可判定点(2,-6)在曲线y=f(x)上.
∵f′(x)=(x3+x-16)′=3x2+1,
∴在点(2,-6)处的切线的斜率为k=f′(2)=13.
∴切线的方程为y=13(x-2)+(-6),
即y=13x-32.
(2)法一:设切点为(x0,y0),
则直线l的斜率为f′(x0)=3 +1,
+1,
∴直线l的方程为y=(3 +1)(x-x0)+
+1)(x-x0)+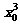 +x0-16,
+x0-16,
又∵直线l过点(0,0),
∴0=(3 +1)(-x0)+
+1)(-x0)+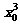 +x0-16,
+x0-16,
整理得,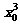 =-8,∴x0=-2,
=-8,∴x0=-2,
∴y0=(-2)3+(-2)-16=-26,
k=3×(-2)2+1=13.
∴直线l的方程为y=13x,切点坐标为(-2,-26).
法二:设直线l的方程为y=kx,切点为(x0,y0),
则k==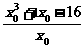 ,
,
又∵k=f′(x0)=3 +1,
+1,
∴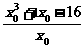 =3
=3 +1,
+1,
解之得x0=-2,
∴y0=(-2)3+(-2)-16=-26,
k=3×(-2)2+1=13.
∴直线l的方程为y=13x,切点坐标为(-2,-26).
(3)∵切线与直线y=-+3垂直,
∴切线的斜率k=4.
设切点的坐标为(x0,y0),则f′(x0)=3 +1=4,
+1=4,
∴x0=±1,
∴或
切线方程为y=4(x-1)-14或y=4(x+1)-18.
即y=4x-18或y=4x-14.
|
题组三 |
导数的灵活应用 |
8.(2009·福建高考)若曲线f(x)=ax2+lnx存在垂直于y轴的切线,则实数a的取值范围是________.
解析:f′(x)=2ax+.
∵f(x)存在垂直于y轴的切线,
∴f′(x)=0有解,即2ax+=0有解,
∴a=-,∴a∈(-∞,0).
答案:(-∞,0)
7.(2009·宁夏、海南高考)曲线y=xex+2x+1在点(0,1)处的切线方程为________________.
解析:y′=ex+x·ex+2,y′|x=0=3,
∴切线方程为y-1=3(x-0),∴y=3x+1.
答案:y=3x+1
6.(2010·福建四地六校联考)下列曲线的所有切线构成的集合中,存在无数对互相垂直的切线的曲线是 ( )
A.f(x)=ex B.f(x)=x3 C.f(x)=lnx D.f(x)=sinx
解析:设切点的横坐标为x1,x2
则存在无数对互相垂直的切线,即f′(x1)·f′(x2)=-1有无数对x1,x2使之成立
对于A由f′(x)=ex>0,
所以不存在f′(x1)·f′(x2)=-1成立;
对于B由于f′(x)=3x2>0,
所以也不存在f′(x1)·f′(x2)=-1成立;
对于C由于f(x)=lnx的定义域为(0,+∞),
∴f′(x)=>0,
对于Df′(x)=cosx,∴f′(x1)·f′(x2)=cosx1·cosx2,当x1=2kπ,x2=(2k+1)π,k∈Z,f′(x1)·f′(x2)=-1恒成立.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com