9．不等式(x+1)≥0的解集是________．

解析：∵≥0，∴x≥1.

同时x+1≥0，即x≥－1.∴x≥1.

答案：{x|x≥1}

8．某公司租地建仓库，每月土地占用费y₁与仓库到车站的距离成反比，而每月库存货物的运费y₂与仓库到车站的距离成正比，如果在距离车站10 km处建仓库，这两项费用y₁和y₂分别为2万元和8万元，那么，要使这两项费用之和最小，仓库应建在离车站　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

(　)

A．5 km处 　　　B．4 km处　　　　　 C．3 km处 　　　　　　D．2 km处

解析：由题意可设y₁＝，y₂＝k₂x，

∴k₁＝xy₁，k₂＝，

把x＝10，y₁＝2与x＝10，y₂＝8分别代入上式得k₁＝20，k₂＝0.8，

∴y₁＝，y₂＝0.8x(x为仓库与车站距离)，

费用之和y＝y₁+y₂＝0.8x+≥2 ＝8，

当且仅当0.8x＝，即x＝5时等号成立．

答案：A

第Ⅱ卷　(非选择题，共110分)

6．不等式组，所表示的平面区域的面积等于　　　　　　 　　　　(　)

A.　　　 　　　　　　　　　B.　　　　　　　　　 C. 　　　　　　D.

解析：不等式组表示的平面区域如图所示，

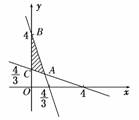由

得交点A的坐标为(1,1)．

又B、C两点的坐标为(0,4)，(0，)．

故S_△ABC＝(4－)×1＝.

答案：C

5．三段论：“①只有船准时起航，才能准时到达目的港；②某艘船是准时到达目的港的；③所以这艘船是准时起航的”中小前提是　　　　　　　　　　　　　　　　 (　)

A．①　 　　B．②　　　　 C．①②　 　　　　D．③

解析：大前提是①，小前提是②，结论是③.

答案：B

4．给出下面类比推理命题(其中Q为有理数集，R为实数集，C为复数集)：

①“若a，b∈R，则a－b＝0⇒a＝b”类比推出“若a，b∈C，则a－b＝0⇒a＝b”；

②“若a，b，c，d∈R，则复数a+bi＝c+di⇒a＝c，b＝d”类比推出“若a，b，c，d∈Q，则a+b＝c+d⇒a＝c，b＝d”；

③“若a，b∈R，则a－b＞0⇒a＞b”类比推出“若a，b∈C，则a－b＞0⇒a＞b”．

其中类比得到的结论正确的个数是　　　　　　　　　　　　　　　　　　　 (　)

A．0　 　　　　　　B．1 　　　　　　C．2 　　　　　　　　D．3

解析：①②是正确的，③是错误的，因为复数不能比较大小，如a＝5+6i，b＝4+6i，虽然满足a－b＝1＞0，但复数a与b不能比较大小．

答案：C

3．若集合A＝{x||2x－1|＜3}，B＝{x|＜0}，则A∩B是　　　　　　　　　 (　)

A．{x|－1＜x＜－或2＜x＜3}　　　　 B．{x|2＜x＜3}

C．{x|－＜x＜2}　　　　　　　　　 D．{x|－1＜x＜－}

解析：∵|2x－1|＜3，∴－3＜2x－1＜3.∴－1＜x＜2.

又∵＜0，∴(2x+1)(x－3)＞0，

∴x＞3或x＜－.∴A∩B＝{x|－1＜x＜－}．

答案：D

2．已知函数f(x)＝，若f(x)≥1，则x的取值范围是　　　　　　 (　)

A．(－∞，－1]　 　　　　　　　B．[1，+∞)

C．(－∞，0]∪[1，+∞) 　　　　D．(－∞，－1]∪[1，+∞)

解析：将原不等式转化为：或，从而得x≥1或x≤－1.

答案：D

1．下列命题中的真命题是　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．若a＞b，c＞d，则ac＞bd　 　　　B．若|a|＞b，则a²＞b²

C．若a＞b，则a²＞b²　 　　　　　　D．若a＞|b|，则a²＞b²

解析：由a＞|b|，可得a＞|b|≥0⇒a²＞b².

答案：D

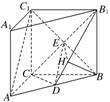
20. (本小题满分14分)(2009·东北四市模拟)如图，正四棱柱ABCD－A₁B₁C₁D₁中，AA₁＝2AB＝4，点E在CC₁上，且CE＝λCC₁.

(1)λ为何值时，A₁C⊥平面BED；

(2)若A₁C⊥平面BED，求二面角A₁－BD－E的余弦值.

解：法一：(1)连接B₁C交BE于点F，连接AC交BD于点G，

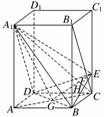∴AC⊥BD，由垂直关系得，A₁C⊥BD，

若A₁C⊥平面BED，则A₁C⊥BE，

由垂直关系可得B₁C⊥BE，

∴△BCE∽△B₁BC，∴＝＝，

∴CE＝1，∴λ＝＝.

(2)连接A₁G，连接EG交A₁C于H，则A₁G⊥BD.

∵A₁C⊥平面BED，

∴∠A₁GE是二面角A₁－BD－E的平面角.

∵A₁G＝3，EG＝，A₁E＝，

∴cos∠A₁GE＝＝，

法二：(1)以D为坐标原点，射线DA为x轴的正半轴，射线DC为y轴的正半轴，射线DD₁为z轴的正半轴，建立如图所示直角坐标系D－xyz.

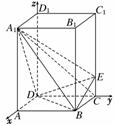依题设，D(0,0,0)，B(2,2,0)，C(0,2,0)，A₁(2,0,4)，

∵CE＝λCC₁＝4λ，∴E(0,2,4λ)，

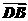∴＝(2,2,0)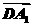，＝(2,0,4)，

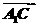＝(－2,2，－4)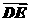，＝(0,2,4λ)，

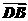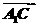∵·＝2×(－2)+2×2+0×(－4)＝0，

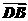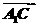∴⊥，∴DB⊥A₁C.

若A₁C⊥平面BED，则A₁C⊥DE，∴⊥，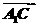

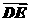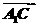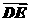∴·＝(－2)×0+2×2+(－4)×4λ＝4－16λ＝0，

∴λ＝.

(2)设向量n＝(x，y，z)是平面DA₁B的一个法向量，

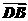则n⊥，n⊥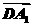，∴2x+2y＝0,2x+4z＝0，

令z＝1，则x＝－2，y＝2，∴n＝(－2,2,1)

由(1)知平面BDE的一个法向量为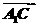＝(－2,2，－4)

∴cos〈n，〉＝＝.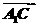

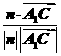即二面角A₁－BD－E的余弦值为.

19. (本小题满分14分)(2009·西安八校联考)如图，在直三棱柱ABC－

A₁B₁C₁中，AC＝BC＝CC₁＝2，AC⊥BC，D为AB的中点.

(1)求证：AC₁∥平面B₁CD；

(2)求二面角B－B₁C－D的正弦值.

解：(1)证明：如图，连接BC₁交B₁C于点E，

则E为BC₁的中点.

∵D为AB的中点，∴在△ABC₁中，AC₁∥DE

又AC₁⊄平面B₁CD，DE⊂平面B₁CD，

∴AC₁∥平面B₁CD

(2)∵AC＝BC，D为AB的中点，

∴CD⊥AB.又平面ABC⊥平面ABB₁A₁，

∴CD⊥平面ABB₁A₁.

∴平面B₁CD⊥平面B₁BD，

过点B作BH⊥B₁D，垂足为H，则BH⊥平面B₁CD，

连接EH，

∵B₁C⊥BE，B₁C⊥EH，

∴∠BEH为二面角B－B₁C－D的平面角.

在Rt△BHE中，BE＝，BH＝＝，

则sin∠BEH＝＝.

即二面角B－B₁C－D的正弦值为.