1．(2009年高考浙江卷改编)设U＝R，A＝{x|x>0}，B＝{x|x>1}，则A∩∁_UB＝____.

解析：∁_UB＝{x|x≤1}，∴A∩∁_UB＝{x|0<x≤1}．答案：{x|0<x≤1}

12．(2008年高考江苏)若f₁(x)＝3^|x－p1|，f₂(x)＝2·3^|x－p2|，x∈R，p₁、p₂为常数，且

f(x)＝(1)求f(x)＝f₁(x)对所有实数x成立的充要条件(用p₁、p₂表示)；(2)设a，b是两个实数，满足a<b，且p₁、p₂∈(a，b)．若f(a)＝f(b)，求证：函数f(x)在区间[a，b]上的单调增区间的长度之和为(闭区间[m，n]的长度定义为n－m)．

解：(1)f(x)＝f₁(x)恒成立⇔f₁(x)≤f₂(x)⇔3^|x－p1|≤2·3^|x－p2|⇔3^{|x－p1|－|x－p2|}≤2

⇔|x－p₁|－|x－p₂|≤log₃2.(*)若p₁＝p₂，则(*)⇔0≤log₃2，显然成立；若p₁≠p₂，记g(x)＝|x－p₁|－|x－p₂|，当p₁>p₂时，g(x)＝

所以g(x)_max＝p₁－p₂，故只需p₁－p₂≤log₃2.

当p₁<p₂时，g(x)＝所以g(x)_max＝p₂－p₁，故只需p₂－p₁≤log₃2.

综上所述，f(x)＝f₁(x)对所有实数x成立的充要条件是|p₁－p₂|≤log₃2.

(2)证明：分两种情形讨论．

①当|p₁－p₂|≤log₃2时，由(1)知f(x)＝f₁(x)(对所有实数x∈[a，b])，则由f(a)＝f(b)及a<p₁<b易知p₁＝.再由f₁(x)＝的单调性可知，f(x)在区间[a，b]上的单调增区间的长度为b－＝.

②当|p₁－p₂|>log₃2时，不妨设p₁<p₂，则p₂－p₁>log₃2.于是，当x≤p₁时，有f₁(x)＝3^p1－x<3^p2－x<f₂(x)，从而f(x)＝f₁(x)．

当x≥p₂时，f₁(x)＝3^x－p1＝3^p2－p1·3^x－p2>3^log₃²·3^x－p2＝f₂(x)，从而f(x)＝f₂(x)．

当p₁<x<p₂时，f₁(x)＝3^x－p1及f₂(x)＝2·3^p₂^－x，由方程3^x₀^－p₁＝2·3^p₂^－x₀，解得f₁(x)与f₂(x)图象交点的横坐标为x₀＝+log₃2.①

显然p₁<x₀＝p₂－[(p₂－p₁)－log₃2]<p₂，这表明x₀在p₁与p₂之间．

由①易知f(x)＝

综上可知，在区间[a，b]上，f(x)＝

故由函数f₁(x)与f₂(x)的单调性可知，f(x)在区间[a，b]上的单调增区间的长度之和为(x₀－p₁)+(b－p₂)，由于f(a)＝f(b)，即3^p₁^－a＝2·3^b－p₂，得

p₁+p₂＝a+b+log₃2.②

故由①②得(x₀－p₁)+(b－p₂)＝b－(p₁+p₂－log₃2)＝.

综合①、②可知，f(x)在区间[a，b]上单调增区间的长度之和为.

11．已知函数f(x)＝.(1)求证：f(x)的图象关于点M(a，－1)对称；

(2)若f(x)≥－2^x在x≥a上恒成立，求实数a的取值范围．

解：(1)证明：设f(x)的图象C上任一点为P(x，y)，则y＝－，

P(x，y)关于点M(a，－1)的对称点为P′(2a－x，－2－y)．

∴－2－y＝－2+＝＝＝，

说明点P′(2a－x，－2－y)也在函数y＝的图象上，由点P的任意性知，f(x)的图象关于点M(a，－1)对称．

(2)由f(x)≥－2^x得≥－2^x，则≤2^x，化为2^x－a·2^x+2^x－2≥0，则有(2^x)²+2^a·2^x－2·2^a≥0在x≥a上恒成立．令g(t)＝t²+2^a·t－2·2^a，则有g(t)≥0在t≥2^a上恒成立．∵g(t)的对称轴在t＝0的左侧，∴g(t)在t≥2^a上为增函数．

∴g(2^a)≥0.∴(2^a)²+(2^a)²－2·2^a≥0，∴2^a(2^a－1)≥0，则a≥0.即实数a的取值范围为a≥0.

10．(2010年宁夏银川模拟)已知函数f(x)＝a^2x+2a^x－1(a>0，且a≠1)在区间[－1,1]上的最大值为14，求实数a的值．

解：f(x)＝a^2x+2a^x－1＝(a^x+1)²－2，∵x∈[－1,1]，

(1)当0<a<1时，a≤a^x≤，∴当a^x＝时，f(x)取得最大值．

∴(+1)²－2＝14，∴＝3，∴a＝.

(2)当a>1时，≤a^x≤a，∴当a^x＝a时，f(x)取得最大值．

∴(a+1)²－2＝14，∴a＝3.综上可知，实数a的值为或3.

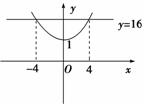
9．函数y＝2^|x|的定义域为[a，b]，值域为[1,16]，当a变动时，函数b＝g(a)的图象可以是________．

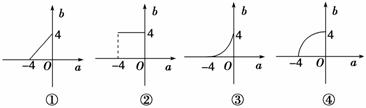
解析：函数y＝2^|x|的图象如图．

当a＝－4时，0≤b≤4，

当b＝4时，－4≤a≤0，答案：②

8．(2009年高考湖南卷改编)设函数y＝f(x)在(－∞，+∞)内有定义，对于给定的正数K，定义函数f_K(x)＝取函数f(x)＝2^－|x|，当K＝时，函数f_K(x)的单调递增区间为________．

解析：由f(x)＝2^－|x|≤得x≥1或x≤－1，∴f_K(x)＝

则单调增区间为(－∞，－1]．答案：(－∞，－1]

7．(2009年高考辽宁卷改编)已知函数f(x)满足：当x≥4时，f(x)＝()^x；当x<4时，f(x)＝f(x+1)，则f(2+log₂3)＝________.

解析：∵2<3<4＝2²，∴1<log₂3<2.∴3<2+log₂3<4，∴f(2+log₂3)

＝f(3+log₂3)＝f(log₂24)＝()log₂24＝2^－log₂24＝2log₂＝.答案：

6．(2009年高考山东卷改编)函数y＝的图象大致为________．

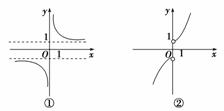
解析：∵f(－x)＝＝－＝－f(x)，∴f(x)为奇函数，排除④.

又∵y＝＝＝＝1+在(－∞，0)、(0，+∞)上都是减函数，排除②、③.答案：①

5．(2010年山东青岛质检)已知f(x)＝()^x，若f(x)的图象关于直线x＝1对称的图象对应的函数为g(x)，则g(x)的表达式为________．

解析：设y＝g(x)上任意一点P(x，y)，P(x，y)关于x＝1的对称点P′(2－x，y)在f(x)＝()^x上，∴y＝()^2－x＝3^x－2.答案：y＝3^x－2(x∈R)

4．(2010年北京朝阳模拟)已知函数f(x)＝a^x(a>0且a≠1)，其反函数为f^－1(x)．若f(2)＝9，则f^－1()+f(1)的值是________．

解析：因为f(2)＝a²＝9，且a>0，∴a＝3，则f(x)＝3^x＝，∴x＝－1，

故f^－1()＝－1.又f(1)＝3，所以f^－1()+f(1)＝2.答案：2