1．(2010年广东江门质检)函数y＝+lg(2x－1)的定义域是________．

解析：由3x－2>0,2x－1>0，得x>.答案：{x|x>}

6．已知函数f(x)＝(1)求f(1－)，f{f[f(－2)]}的值；(2)求f(3x－1)；(3)若f(a)＝， 求a.

解：f(x)为分段函数，应分段求解．

(1)∵1－＝1－(+1)＝－<－1，∴f(－)＝－2+3，

又∵f(－2)＝－1，f[f(－2)]＝f(－1)＝2，∴f{f[f(－2)]}＝1+＝.

(2)若3x－1>1，即x>，f(3x－1)＝1+＝；

若－1≤3x－1≤1，即0≤x≤，f(3x－1)＝(3x－1)²+1＝9x²－6x+2；

若3x－1<－1，即x<0，f(3x－1)＝2(3x－1)+3＝6x+1.

∴f(3x－1)＝

(3)∵f(a)＝，∴a>1或－1≤a≤1.

当a>1时，有1+＝，∴a＝2；

当－1≤a≤1时，a²+1＝，∴a＝±.

∴a＝2或±.

B组

5．(原创题)由等式x³+a₁x²+a₂x+a₃＝(x+1)³+b₁(x+1)²+b₂(x+1)+b₃定义一个映射f(a₁，a₂，a₃)＝(b₁，b₂，b₃)，则f(2,1，－1)＝________.

解析：由题意知x³+2x²+x－1＝(x+1)³+b₁(x+1)²+b₂(x+1)+b₃，

令x＝－1得：－1＝b₃；

再令x＝0与x＝1得，

解得b₁＝－1，b₂＝0.

答案：(－1,0，－1)

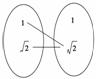
4．(2010年黄冈市高三质检)函数f：{1，}→{1，}满足f[f(x)]>1的这样的函数个数有________个．

解析：如图．答案：1

3．(2009年高考北京卷)已知函数f(x)＝若f(x)＝2，则x＝________.

解析：依题意得x≤1时，3^x＝2，∴x＝log₃2；

当x>1时，－x＝2，x＝－2(舍去)．故x＝log₃2.答案：log₃2

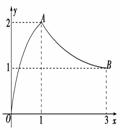
2．(2010年绍兴第一次质检)如图，函数f(x)的图象是曲线段OAB，其中点O，A，B的坐标分别为(0,0)，(1,2)，(3,1)，则f()的值等于________．

解析：由图象知f(3)＝1，f()＝f(1)＝2.答案：2

1．(2009年高考江西卷改编)函数y＝的定义域为________．

解析：⇒x∈[－4,0)∪(0,1]

答案：[－4,0)∪(0,1]

12．已知：f(x)＝log₃，x∈(0，+∞)，是否存在实数a，b，使f(x)同时满足下列三个条件：(1)在(0,1]上是减函数，(2)在[1，+∞)上是增函数，(3)f(x)的最小值是1.若存在，求出a、b；若不存在，说明理由．

解：∵f(x)在(0,1]上是减函数，[1，+∞)上是增函数，∴x＝1时，f(x)最小，log₃＝1.即a+b＝2.

设0＜x₁＜x₂≤1，则f(x₁)＞f(x₂)．即＞恒成立．

由此得＞0恒成立．

又∵x₁－x₂＜0，x₁x₂＞0，∴x₁x₂－b＜0恒成立，∴b≥1.

设1≤x₃＜x₄，则f(x₃)＜f(x₄)恒成立．∴＜0恒成立．

∵x₃－x₄＜0，x₃x₄＞0，∴x₃x₄＞b恒成立．∴b≤1.由b≥1且b≤1可知b＝1，∴a＝1.∴存在a、b，使f(x)同时满足三个条件．

11．(2010年广西河池模拟)已知定义在区间(0，+∞)上的函数f(x)满足f()＝f(x₁)－f(x₂)，且当x>1时，f(x)<0.

(1)求f(1)的值；(2)判断f(x)的单调性；(3)若f(3)＝－1，解不等式f(|x|)<－2.

解：(1)令x₁＝x₂>0，代入得f(1)＝f(x₁)－f(x₁)＝0，故f(1)＝0.

(2)任取x₁，x₂∈(0，+∞)，且x₁>x₂，则>1，由于当x>1时，f(x)<0，

所以f()<0，即f(x₁)－f(x₂)<0，因此f(x₁)<f(x₂)，

所以函数f(x)在区间(0，+∞)上是单调递减函数．

(3)由f()＝f(x₁)－f(x₂)得f()＝f(9)－f(3)，而f(3)＝－1，所以f(9)＝－2.

由于函数f(x)在区间(0，+∞)上是单调递减函数，

由f(|x|)<f(9)，得|x|>9，∴x>9或x<－9.因此不等式的解集为{x|x>9或x<－9}．

10．试讨论函数y＝2(logx)2－2logx+1的单调性．

解：易知函数的定义域为(0，+∞)．如果令u＝g(x)＝logx，y＝f(u)＝2u²－2u+1，那么原函数y＝f[g(x)]是由g(x)与f(u)复合而成的复合函数，而u＝logx在x∈(0，+∞)内是减函数，y＝2u²－2u+1＝2(u－)²+在u∈(－∞，)上是减函数，在u∈(，+∞)上是增函数．又u≤，即logx≤，得x≥；u>，得0<x<.由此，从下表讨论复合函数y＝f[g(x)]的单调性：

函数	单调性
(0，)	(，+∞)
u＝logx
f(u)＝2u2－2u+1	?	?
y＝2(logx)2－2logx+1	?	?

故函数y＝2(logx)²－2logx+1在区间(0，)上单调递减，在区间(，+∞)上单调递增．