3．(2010年福建厦门检测)已知一个球与一个正三棱柱的三个侧面和两个底面相切，若这个球的体积是，则这个三棱柱的体积是________．

解析：由πR³＝，得R＝2.∴正三棱柱的高h＝4.设其底面边长为a，则·a＝2.∴a＝4.∴V＝(4)²·4＝48.答案：48

2．在三棱锥A－BCD中，侧棱AB、AC、AD两两垂直，△ABC，△ACD，△ADB的面积分别为，，，则该三棱锥的体积为________．

解析：AB·AC＝，AD·AC＝，AB·AD＝，∴AB＝，AC＝1，AD＝.∴V＝··1··＝.答案：

1．(2008年高考湖北卷)用与球心距离为1的平面去截球，所得的截面面积为π，则球的体积为________．

解析：截面圆的半径为1，又球心到截面距离等于1，所以球的半径R＝，故球的体积V＝πR³＝π.答案：

6．在长方体ABCD－A₁B₁C₁D₁中，AB＝BC＝2，过A₁、C₁、B三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD－A₁C₁D₁，且这个几何体的体

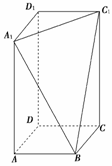积为.(1)证明：直线A₁B∥平面CDD₁C₁；(2)求棱A₁A的长；(3)求经过A₁，C₁，B，D四点的球的表面积．

解：(1)证明：法一：如图，连结D₁C，

∵ABCD－A₁B₁C₁D₁是长方体，

∴A₁D₁∥BC且A₁D₁＝BC.

∴四边形A₁BCD₁是平行四边形．

∴A₁B∥D₁C.

∵A₁B⊄平面CDD₁C₁，D₁C⊂平面CDD₁C₁，

∴A₁B∥平面CDD₁C₁.

法二：∵ABCD－A₁B₁C₁D₁是长方体，

∴平面A₁AB∥平面CDD₁C₁.

∵A₁B⊂平面A₁AB，A₁B⊄平面CDD₁C₁.

∴A₁B∥平面CDD₁C₁.

(2)设A₁A＝h，∵几何体ABCD－A₁C₁D₁的体积为，

∴VABCD－A₁C₁D₁＝VABCD－A₁B₁C₁D₁－VB－A₁B₁C₁＝，

即S_ABCD×h－×S△A₁B₁C₁×h＝，

即2×2×h－××2×2×h＝，解得h＝4.

∴A₁A的长为4.

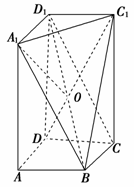
(3)如图，连结D₁B，设D₁B的中点为O，连OA₁，OC₁，OD.

∵ABCD－A₁B₁C₁D₁是长方体，∴A₁D₁⊥平面A₁AB.

∵A₁B⊂平面A₁AB，∴A₁D₁⊥A₁B.

∴OA₁＝D₁B.同理OD＝OC₁＝D₁B.

∴OA₁＝OD＝OC₁＝OB.

∴经过A₁，C₁，B，D四点的球的球心为点O.

∵D₁B²＝A₁D₁²+A₁A²+AB²＝2²+4²+2²＝24.

∴S_球＝4π×(OD₁)²＝4π×()²＝π×D₁B²＝24π.

故经过A₁，C₁，B，D四点的球的表面积为24π.

B组

5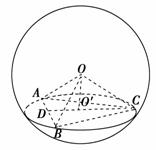．已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半，且AC＝BC＝6，AB＝4，则球的半径等于________，球的表面积等于________．

解析：如右图，设球的半径为r，O′是△ABC的外心，外接圆半径为R，则OO′⊥面ABC.在Rt△ACD中，cosA＝，则sinA＝.在△ABC中，由正弦定理得＝2R，R＝，即O′C＝.

在Rt△OCO′中，由题意得r²－r²＝，得r＝.球的表面积S＝4πr²＝4π×＝54π.

答案：　54π

4．矩形ABCD中，AB＝4，BC＝3，沿AC将矩形ABCD折成一个直二面角B－AC－D，则四面体ABCD的外接球的体积为________．

解析：由题意知，球心到四个顶点的距离相等，所以球心在对角线AC上，且其半径为AC长度的一半，则V_球＝π×()³＝.答案：

3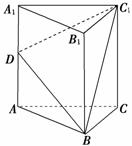．(2010年南京调研)如图，在正三棱柱ABC－A₁B₁C₁中，D为棱AA₁的中点．若截面△BC₁D是面积为6的直角

三角形，则此三棱柱的体积为________．

解析：设AC＝a，CC₁＝b，则由BC₁²＝BC²+CC₁²，BC₁²＝DC₁²+DB²，即得(a²+b²)×2＝a²+b²，得b²＝2a²，又×a²＝6，∴a²＝8，∴V＝×8×4＝8.

答案：8

2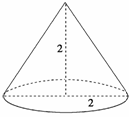．(2009年高考上海卷)若等腰直角三角形的直角边长为2，则以一直角边所在的直线为轴旋转一周所成的几何体体积是_________．

解析：如图为等腰直角三角形旋转而成的旋转体．

V＝S·h＝πR²·h

＝π×2²×2＝.答案：

1．(2010年东北四校联考)已知一个长方体的同一顶点处的三条棱长分别为1，，2，则其外接球的表面积为________．

解析：设外接球半径为r，则(2r)²＝1²+()²+2²＝8，故r²＝2.∴S_球＝4πr²＝8π.答案：8π

12．若直线l过点P(3,0)且与两条直线l₁：2x－y－2＝0，l₂：x+y+3＝0分别相交于两点A、B，且点P平分线段AB，求直线l的方程．

解：设A(m,2m－2)，B(n，－n－3)．∵线段AB的中点为P(3,0)，

∴∴∴∴A(，)，

∴直线l的斜率k＝＝8，

∴直线l的方程为y－0＝8(x－3)，即8x－y－24＝0