1．(2010年宁波十校联考)设b、c表示两条直线，α，β表示两个平面，则下列命题是真命题的是________．

①若b⊂α，c∥α，则b∥c　②若b⊂α，b∥c，则c∥α

③若c∥α，α⊥β，则c⊥β　 ④若c∥α，c⊥β，则α⊥β

解析：①中，b，c亦可能异面；②中，也可能是c⊂α；③中，c与β的关系还可能是斜交、平行或c⊂β；④中，由面面垂直的判定定理可知正确．

答案：④

12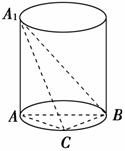．(2010年广州质检)如图，A₁A是圆柱的母线，AB是圆柱底面圆的直径，C是底面圆周上异于A、B的任意一点，A₁A＝AB＝2.

(1)求证：BC⊥平面A₁AC；

(2)求三棱锥A₁－ABC的体积的最大值．

解：(1)证明：∵C是底面圆周上异于A、B的任意一点，且AB是圆柱底面圆的直径，

∴BC⊥AC.

∵AA₁⊥平面ABC，BC平面ABC，

∴AA₁⊥BC.

∵AA₁∩AC＝A，AA₁平面AA₁C，AC平面AA₁C，

∴BC⊥平面AA₁C.

(2)设AC＝x，在Rt△ABC中，

BC＝＝(0＜x＜2)，

故VA₁－ABC＝S_△ABC·AA₁＝··AC·BC·AA₁

＝x(0＜x＜2)，

即VA₁－ABC＝x＝

＝.

∵0＜x＜2,0＜x²＜4，∴当x²＝2，即x＝时，

三棱锥A₁－ABC的体积最大，其最大值为.

11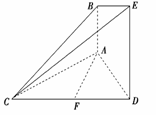．如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD＝DE＝2AB＝2，F为CD的中点．

(1)求证：AF⊥平面CDE；

(2)求证：AF∥平面BCE；

(3)求四棱锥C－ABED的体积．

解：(1)证明：∵F为等边三角形CD边上的中点，

∴AF⊥CD，

∵DE⊥平面ACD，AF⊂平面ACD，

∴AF⊥DE，

又CD∩DE＝D，∴AF⊥平面CDE.

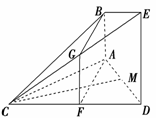(2)证明：取CE的中点G，连FG、BG.∵F为CD的中点，

∴GF∥DE且GF＝DE.

∵AB⊥平面ACD，DE⊥平面ACD，

∴AB∥DE，∴GF∥AB.

又AB＝DE，∴GF＝AB.

∴四边形GFAB为平行四边形，则AF∥BG.

∵AF⊄平面BCE，BG⊂平面BCE，∴AF∥平面BCE.

(3)取AD中点M，连结CM，

∵△ACD为等边三角形，则CM⊥AD，

∵DE⊥平面ACD，且DE⊂平面ABED，

∴平面ACD⊥平面ABED，

又平面ACD∩平面ABED＝AD，∴CM⊥平面ABED，

∴CM为四棱锥C－ADEB的高，

∴V＝CM·S_ABED＝AF·S_ABED＝.

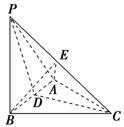
10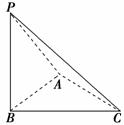．(2009年高考宁夏、海南卷)如图，在三棱锥P－ABC中，△PAB是等边三角形，∠PAC＝∠PBC＝90°.

(1)证明：AB⊥PC；

(2)若PC＝4，且平面PAC⊥平面PBC，求三棱锥P－ABC的体积．

解：(1)证明：因为△PAB是等边三角形，

∠PAC＝∠PBC＝90°，

所以Rt△PBC≌Rt△PAC，可得AC＝BC.

如图，取AB中点D，连结PD、CD，

则PD⊥AB，CD⊥AB，所以AB⊥平面PDC，

所以AB⊥PC.

(2)作BE⊥PC，垂足为E，连结AE.

因为Rt△PBC≌Rt△PAC，

所以AE⊥PC，AE＝BE.

由已知，平面PAC⊥平面PBC，故∠AEB＝90°.

因为Rt△AEB≌Rt△PEB，

所以△AEB，△PEB，△CEB都是等腰直角三角形．

由已知PC＝4，得AE＝BE＝2，

△AEB的面积S＝2.

因为PC⊥平面AEB，

所以三棱锥P－ABC的体积V＝×S×PC＝.

9．(2010年南通调研)正方体ABCD－A₁B₁C₁D₁的棱长为2，则四面体A－B₁CD₁的外接球的体积为________．

解析：四面体A－B₁CD₁的外接球即为正方体的外接球，所以2r＝.∴r＝3，V_球＝πr³＝π×27＝36π.答案：36π

8．在一个锥体中，作平行于底面的截面，若这个截面面积与底面面积之比为1∶3，则锥体被截面所分成的两部分的体积之比为________

解析：利用一个锥体被平行于底面的截面所截得的小锥体与原锥体体积之比等于相似比的立方，而这个截面面积与底面面积之比等于相似比的平方．

答案：1∶3

7．若长方体的三个共顶点的面的面积分别是，，，则长方体的体积是__．

解析：可设长方体同一个顶点上的三条棱长分别为a，b，c，列出方程组解得所以长方体的体积V＝1××＝.

6．(2009年高考江西卷)体积为8的一个正方体，其全面积与球O的表面积相等，则球O的体积等于________．

解析：设正方体棱长为a，则a³＝8，∴a＝2.

∵S_正方体＝S_球，∴6×2²＝4πR²，∴R＝ .

V_球＝πR³＝π( )³＝.答案：

5．(2009年高考全国卷Ⅰ)已知OA为球O的半径，过OA的中点M且垂直于OA的平面截球面得到圆M.若圆M的面积为3π，则球O的表面积等于__________．

解析：由题意得圆M的半径r＝，又球心到圆M的距离为，由勾股定理得R²＝r²+()²，∴R＝2，则球的表面积为4π×2²＝16π.答案：16π

4．(2009年高考陕西卷改编)若正方体的棱长为，则以该正方体各个面的中心为顶点的凸多面体的体积为________．

解析：所求八面体体积是两个底面边长为1，高为的四棱锥的体积和，一个四棱锥体积V₁＝×1×＝，故八面体体积V＝2V₁＝.答案：