12．甲、乙两艘轮船都要停靠在同一个泊位，它们可能在一昼夜的任意时刻到达．甲、乙两船停靠泊位的时间分别为4小时与2小时，求有一艘船停靠泊位时必需等待一段时间的概率．

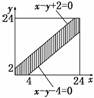解：甲比乙早到4小时内乙需等待，甲比乙晚到2小时内甲需等待．

以x和y分别表示甲、乙两船到达泊位的时间，则有一

艘船停靠泊位时需等待一段时间的充要条件为－2≤x－y≤4，在如

图所示的平面直角坐标系内，(x，y)的所有可能结果是边长为24的

正方形，而事件A“有一艘船停靠泊位时需等待一段时间”的可能结果由阴影部分表示．由几何概型公式得：

P(A)＝＝.

故有一艘船停靠泊位时必需等待一段时间的概率是.

11．在平面直角坐标系xOy中，设D是横坐标与纵坐标的绝对值均不大于2的点构成的区域，E是到原点的距离不大于1的点构成的区域，向D中随机投一点，则所投的点落在E中的概率是__________．

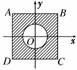解析：如图：区域D表示边长为4的正方形ABCD的内部(含边界)，

区域E表示单位圆及其内部，因此P＝＝.

答案：

10.平面上有一组平行线且相邻平行线间的距离为3 cm，把一枚半径为1 cm的硬币任意平掷在这个平面，则硬币不与任何一条平行线相碰的概率是　　　　　　　　 (　)

A. 　　　　　　　　　B.　　　　　　　　 C. 　　　　　　　　　D.

解析：平面被这一组平行线分割成条状区域，现对两条平行线之间的区域考虑：平行线间的距离为3 cm，硬币半径为1 cm，要想硬币不与两条平行线相碰，硬币中心与两条平行线的距离都应大于1 cm，如图：

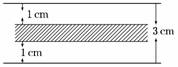
硬币中心只有落在阴影部分(不包括边界)时，才能让硬币与两条平行线都不相碰，则硬币中心落在阴影部分的概率为.整个平面由无数个这样的条状区域组成，故所求概率是.

答案：B

9．已知函数f(x)＝x²－2ax+b²，a，b∈R.

(1)若a从集合{0,1,2,3}中任取一个元素，b从集合{0,1,2}中任取一个元素，求方程f(x)＝0有两个不相等实根的概率；

(2)若a从区间中任取一个数，b从区间中任取一个数，求方程f(x)＝0没有实根的概率．

解：(1)∵a取集合{0,1,2,3}中任一个元素，b取集合{0,1,2}中任一个元素，

∴a，b的取值的情况有(0,0)，(0,1)，(0,2)，(1,0)，(1,1)，(1,2)，(2,0)，(2,1)，(2,2)，(3,0)，(3,1)，(3,2)．

其中第一个数表示a的取值，第二个数表示b的取值，

即基本事件总数为12.

设“方程f(x)＝0有两个不相等的实根”为事件A，

当a≥0，b≥0时，方程f(x)＝0有两个不相等实根的充要条件为a＞b.

当a＞b时，a，b取值的情况有(1,0)，(2,0)，(2,1)，(3,0)，(3,1)，(3,2)，

即A包含的基本事件数为6，

∴方程f(x)＝0有两个不相等实根的概率

P(A)＝＝.

(2)∵a从区间中任取一个数，b从区间中任取一个数，则试验的全部结果构成区域Ω＝{(a，b)|0≤a≤2,0≤b≤3}，

这是一个矩形区域，其面积S_Ω＝2×3＝6.

设“方程f(x)＝0没有实根”为事件B，则事件B所构成的区域为

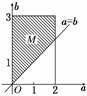M＝{(a，b)|0≤a≤2,0≤b≤3，a＜b}，

即图中阴影部分的梯形，其面积

S_M＝6－×2×2＝4.

由几何概型的概率计算公式可得方程f(x)＝0没有实根的概率P(B)＝＝＝.

8．(2010·济南模拟)在边长为2的正三角形ABC内任取一点P，则使点P到三个顶点的距离至少有一个小于1的概率是________．

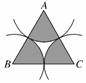解析：以A、B、C为圆心，以1为半径作圆，与△ABC相交出

三个扇形(如图所示)，

当P落在阴影部分时符合要求．

∴P＝＝.

答案：π

7．在区域内任取一点P，则点P落在单位圆x²+y²＝1内的概率为(　)

A.　 　　　　　　　　B.　　　　　　　　　　　 C. 　　　　　　　　　　D.

解析：区域为△ABC内部(含边界)，则概率为

P＝＝＝.

答案：D

6．已知Ω＝{(x，y)|x+y≤6，x≥0，y≥0}，A＝{(x，y)|x≤4，y≥0，x－2y≥0}，若向区域Ω上随机投一点P，则点P落入区域A的概率为　 　　　　　　　　　　　(　)

A.　　　　　　 　B.　　　　　　　 C.　 　　　　　　　D.

解析：作出两集合表示的平面区域如图所示．容易得出

Ω所表示的平面区域为三角形AOB及其边界，A表示的

区域为三角形OCD及其边界．

容易求得D(4,2)恰为直线x＝4，x－2y＝0，x+y＝6三线的交点．

则可得S_△AOB＝×6×6＝18，S_△OCD＝×4×2＝4.

所以点P落在区域A的概率为＝.

答案：D

5．设－1≤a≤1，－1≤b≤1，则关于x的方程x²+ax+b²＝0有实根的概率是　　 (　)

A. 　　　　　　　　B.　　　　　　　　 C.　 　　　　　　　　　D.

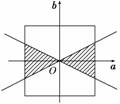解析：由题知该方程有实根满足条件作平面

区域如右图：由图知阴　 影面积为1，总的事件对应面积为正方

形的面积，故概率为.

答案：B

4.(2009·辽宁高考)ABCD为长方形，AB＝2，BC＝1，O为AB的中点．在长方形ABCD内随机取一点，取到的点到O的距离大于1的概率为　　　　　　　　　　　 (　)

A.　　　　　　 　B．1－　　　　　　　 C. 　　　　　　　　D．1－

解析：对应长方形的面积为2×1＝2，而取到的点到O的距离小于等于1时，其是以O为圆心，半径为1所作的半圆，对应的面积为×π×1²＝π，那么满足条件的概率为：1－＝1－.

答案：B

3．《广告法》对插播广告的时间有一定的规定，某人对某台的电视节目做了长期的统计后得出结论，他任意时间打开电视机看该台节目，看不到广告的概率为，那么该台每小时约有________分钟的广告．

解析：60×(1－)＝6分钟．

答案：6