10．(2010·贵阳模拟)(+)ⁿ的展开式中，各项系数的和与其各项二项式系数的和之比为64，则(1－x)ⁿ的展开式中系数最小的项的系数等于________．

解析：展开式中，各项系数的和为4ⁿ，各项二项式系数的和为2ⁿ，由已知得2ⁿ＝64，所以n＝6，(1－x)⁶的展开式中，第四项的系数最小，为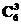－＝－20.

答案：－20

9.在ⁿ的展开式中，只有第5项的二项式系数最大，则展开式的常数项为(　)

A．－7 　　　　　　　B．7 　　　　　　　　　C．－28 　　　　　　　D．28

解析：依题意，+1＝5，∴n＝8.二项式为⁸，易得常数项为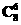²⁶＝7.

答案：B

8．若(x－2)⁵＝a₅x⁵+a₄x⁴+a₃x³+a₂x²+a₁x+a₀，则a₁+a₂+a₃+a₄+a₅＝________.(用数字作答)

解析：由题设令x＝0得a₀＝(－2)⁵＝－32，

令x＝1得a₅+a₄+a₃+a₂+a₁+a₀＝(1－2)⁵＝－1，

故a₁+a₂+a₃+a₄+a₅＝－1－(－32)＝31.

答案：31

7．(2010·黄石模拟)(1+ax+by)ⁿ展开式中不含x的项的系数绝对值的和为243，不含y的项的系数绝对值的和为32，则a，b，n的值可能为　　　　　　　　　　　 (　)

A．a＝2，b＝－1，n＝5　 　　　　　　　B．a＝－2，b＝－1，n＝6

C．a＝－1，b＝2，n＝6　 　　　　　　　D．a＝1，b＝2，n＝5

解析：不含x的项的系数的绝对值为(1+|b|)ⁿ＝243＝3⁵，不含y的项的系数的绝对值为(1+|a|)ⁿ＝32＝2⁵，

∴n＝5，

答案：D

6．(2009·陕西高考)若(1－2x)²⁰⁰⁹＝a₀+a₁x+…+a₂₀₀₉x²⁰⁰⁹(x∈R)，则++…+的值为　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　 　 　　　　　　　　　　　　　　　　　　　　　　　 　(　)

A．2 　　　　　　　　　B．0 　　　　　　　　C．－1　　　　　　　 　D．－2

解析：令x＝0，则a₀＝1，

令x＝，

则a₀+++…+＝0，

∴++…+＝－1.

答案：C

5.在ⁿ的展开式中，所有奇数项的系数之和为1 024，则中间项系数是(　)

A．330　　　　　　 　B．462 　　　　　　　C．682 　　　　　　　　　D．792

解析：∵二项式的展开式的所有项的二项式系数和为2ⁿ，而所有偶数项的二项式系数和与所有奇数项的二项式系数和相等．由题意得，2＝1 024，∴n＝11，∴展开式共有12项，中间项为第六项、第七项，系数为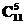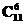＝＝462.

答案：B

4．若⁶的二项展开式中x³的系数为，则a＝__________(用数字作答)．

解析：通项T_r+1＝·，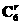

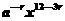当12－3r＝3时，r＝3，

所以系数为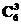·a^－3＝，得a＝2.

答案：2

3．(2009·湖南高考)在(1+x)³+(1+)³+(1+)³的展开式中，x的系数为________(用数字作答)．

解析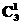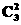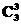：++＝2³－1＝7.

答案：7

2．(x－)¹²的展开式中的常数项为　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 　　 (　)

A．－132 0　 　　　　　B．1 320 　　　　　　　C．－220　　　　　　 　D．220

解析：展开式的通项是T_r+1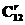＝x^12－r(－)^r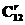＝ (－1)^rx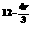，令12－＝0，得r＝9，故展开式的常数项是T₁₀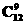＝(－1)⁹＝－220.

答案：C

1.(2009·重庆高考)(x²+)⁸的展开式中x⁴的系数是　　　　　　　　　　　　　　　　　　　　　　 (　)

A．16 　　　　　　B．70 　　　　　　　　C．560 　　　　　　　　　D．1 120

解析：由二项展开式通项公式得

T_r+1＝ (x²)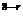()^r＝2^r.

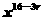由16－3r＝4，r＝4，则x⁴的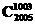系数为2⁴＝1 120.

答案：D