3．点(3,1)和(－4,6)在直线3x－2y+a＝0的两侧，则a的取值范围是________．

解析：点(3,1)和(－4,6)在直线3x－2y+a＝0的两侧，说明将这两点坐标代入3x－2y+a后，符号相反，

所以(9－2+a)(－12－12+a)＜0，

解之得－7＜a＜24.

答案：(－7,24)

2．已知D是由不等式组所确定的平面区域，则圆x²+y²＝4在区域D内的弧长为　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　(　)

A. 　　　　　　B.　　　　　 C. 　　　　　　　D.

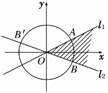解析：如图，l₁、l₂的斜率分别是k₁＝，k₂＝－，不等式组表示的平面区域为阴影部分．

∵tan∠AOB＝＝1，

∴∠AOB＝，∴弧长＝·2＝.

答案：B

1.(2009·福建高考)在平面直角坐标系中，若不等式组(a为常数)所表示的平面区域的面积等于2，则a的值为　　　　　　　　　　　　　　　　　 (　)

A．－5　　　　　　　　 　B．1

C．2　 　　　　　　　　　D．3

解析：不等式组所围成的区域如图所示．

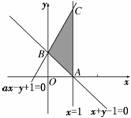
则A(1,0)，B(0,1)，C(1,1+a)

且a>－1，∵S_△ABC＝2，∴(1+a)×1＝2，解得a＝3.

答案：D

2．设A、B为两个事件，若事件A和B同时发生的概率为，在事件A发生的条件下，事件B发生的概率为，则事件A发生的概率为________________．

解析：由题意知，P(AB)＝，P(B|A)＝，

∴P(A)＝＝＝.

1.已知盒中装有3只螺口与7只卡口灯泡，这些灯泡的外形与功率都相同且灯口向下放着，现需要一只卡口灯泡，电工师傅每次从中任取一只并不放回，则在他第1次抽到的是螺口灯泡的条件下，第2次抽到的是卡口灯泡的概率为　　　　　　　　 (　)

A. 　　　　　B.　　　　　　　　　　 C.　 　　　　　　　　　D.

解析：设事件A为“第1次抽到是螺口灯泡”，事件B为“第2次抽到是卡口灯泡”，则P(A)＝，P(AB)＝×＝＝.在已知第1次抽到螺口灯泡的条件下，第2次抽到卡口灯泡的概率为P(B|A)＝＝＝.

答案：D

15．关于二项式(x－1)^{2 005}，有下列命题：

①该二项展开式中非常数项的系数之和是1；

②该二项展开式中第六项为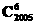x^{1 999}；

③该二项展开式中系数最大的项是第1 002项；

④当x＝2 006时，(x－1)^{2 005}除以2 006的余数是2 005.

其中正确命题的序号是________．(注：把你认为正确的命题序号都填上)

解析：二项式(x－1)^{2 005}所有项的系数和为0，其常数项为－1，非常数项的系数和是1，即得①正确；二项展开式的第六项为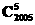－x^{2 000}，即得②错误；二项展开式中系数绝对值最大的项为C_{2 005}x^{1 003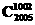}＝x^{1 003}，－C_{2 005}x^{1 002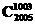}＝－x^{1 002}，得系数最大的项是第1 003项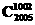·x^{1 003}，即③错误；当x＝2 006时，(x－1)^{2 005}除以2 006的余数是2 006－1＝2 005，即④正确．

答案：①④

14．已知(xcosθ+1)⁵的展开式中x²的系数与(x+)⁴的展开式中x³的系数相等，则cosθ＝__________.

解析：(xcosθ+1)⁵＝(1+xcosθ)⁵，展开式中x²的系数为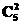cos²θ.

(x+)⁴＝(+x)⁴，展开式中x³的系数为，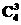

由题意可知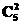cos²θ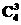＝，∴cos²θ＝，

∴cosθ＝±.

答案：±

13．令a_n为(1+x)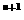的展开式中含x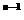项的系数，则数列{}的前n项和为　 (　)

A.　 　　　　B.　　　　　　　　 C.　　　　　　 　D.

解析：∵T_r+1＝C·x^r，

∴a_n＝＝C＝，＝，

∴＝2

＝2＝.

答案：D

12.若(x－)ⁿ的展开式中含有非零常数项，则这样的正整数n的最小值是(　)

A．3　 　　　　　　　　B．4 　　　　　　　　　C．10　 　　　　　　　　D．12

解析：T_r+1＝C(x)^n－r(－)^r

＝C()^n－r(－1)^r()^r·x^n－r·x－

＝C()^n－r(－)^rxn－，

令n－r＝0，得n＝r.

∴n取最小值为4.

答案：B

11．二项式(1+sinx)ⁿ的展开式中，末尾两项的二项式系数之和为7，且二项式系数最大的一项的值为，则x在(0,2π)内的值为________．

解析：由已知可得C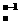+C＝n+1＝7，即得n＝6，

二项式系数最大的一项为

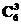·sin³x＝20sin³x＝，

解得sinx＝，又x∈(0,2π)，

∴x＝或.

答案：或