8.(2010·淄博模拟)在正方体ABCD－A₁B₁C₁D₁的侧面AB₁内有一动点P到直线A₁B₁与直线BC的距离相等，则动点P所在曲线的形状为　　　　　　　　　　　　 (　)

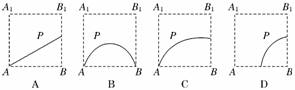
解析：到定点B的距离等于到直线A₁B₁的距离，所以动点P的轨迹是以B为焦点，以A₁B₁为准线的过A的抛物线的一部分．

答案：C

7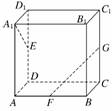．如图，长方体ABCD－A₁B₁C₁D₁中，AA₁＝AB＝2，

AD＝1，点E、F、G分别是DD₁、AB、CC₁的中

点．求异面直线A₁E与GF所成角的大小．

解：连结B₁G，EG，

由于E、G分别是DD₁和CC₁的中点，

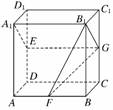∴EG綊C₁D₁，而C₁D₁綊A₁B₁，

∴EG綊A₁B₁，

∴四边形EGB₁A₁是平行四边形．

∴A₁E∥B₁G，从而∠B₁GF为异面直线所成角，

连结B₁F，则FG＝，B₁G＝，B₁F＝，

由FG²+B₁G²＝B₁F²，

∴∠B₁GF＝90°，

即异面直线A₁E与GF所成的角为90°.

6．(文)如图所示，在正四棱柱ABCD－A₁B₁C₁D₁中，E、F分别是AB₁、BC₁的中点，则以下结论中不成立的是　　　　　　　　　　　　　　　　　　　　　 (　)

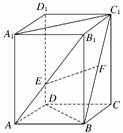
A．EF与BB₁垂直　 　　　　　　　　　　　B．EF与BD垂直

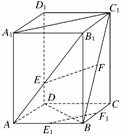C．EF与CD异面　 　　　　　　　　　　　D．EF与A₁C₁异面

解析：设AB的中点为E₁，BC的中点为F₁，

则EF∥E₁F₁，

而E₁F₁⊥BD，E₁F₁⊥BB₁

∴EF⊥BB₁，EF⊥BD，

∴A、B项正确．

又由EF∥E₁F₁知EF∥平面ABCD

∴EF与CD异面，C项正确．

∴易知EF∥A₁C₁，D项错误．

答案：D

(理)(2010·南昌模拟)如图所示，在正三棱柱ABC－A₁B₁C₁

中，D是AC的中点，AA₁∶AB＝∶1，则异面直线AB₁

与BD所成的角为________．

解析：取A₁C₁的中点D₁，连结B₁D₁，

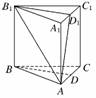由于D是AC的中点，∴B₁D₁∥BD，

∴∠AB₁D₁即为异面直线AB₁与BD所成的角．

连结AD₁，设AB＝a，则AA₁＝a，

∴AB₁＝a，B₁D₁＝a，AD₁＝ ＝a.

∴cos∠AB₁D₁＝＝，

∴∠AB₁D₁＝60°.

答案：60°

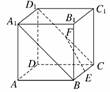
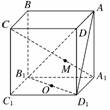
5．(2010·沈阳模拟)正方体AC₁中，E、F分别是线段BC、C₁D的中点，则直线A₁B与

直线EF的位置关系是　　　　　　　　　　　　　　　　　　　　　　 (　)

A．相交 　　　　　　B．异面　　　　　 C．平行　 　　　　　　　D．垂直

解析：如图所示，直线A₁B与直线外一点E确定的平面为A₁BCD₁，EF⊂平面A₁BCD₁，且两直线不平行，故两直线相交．

答案：A

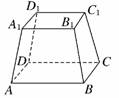
4.在四棱台ABCD－A₁B₁C₁D₁中，上下底面均为正方形，则DD₁与BB₁所在直线是 (　)

A．相交直线 　　　　　　　　　　B．平行直线

C. 不垂直的异面直线　　　　　 　D．互相垂直的异面直线

解析：四棱台可看作是由四棱锥截得的，因此DD₁与BB₁所在直线是相交的．

答案：A

3．如图，在四边形ABCD中，已知AB∥CD，直线

AB、BC、AD、DC分别与平面α相交于点E、G、

H、F.

求证：E、F、G、H四点共线(在同一条直线上)．

证明：∵AB∥CD，∴AB、CD确定一个平面β.

又∵AB∩α＝E，AB⊂β，∴E∈α，E∈β，

即E为平面α与β的一个公共点．

同理可证F、G、H均为平面α与β的公共点．

∵两个平面有公共点，它们有且只有一条通过公共点的公共直线，

∴E、F、G、H四点必定共线．

2．对于空间三条直线，有下列四个条件：

①三条直线两两相交且不共点；

②三条直线两两平行；

③三条直线共点；

④有两条直线平行，第三条直线和这两条直线都相交．

其中，使三条直线共面的充分条件有________．

解析：①中两直线相交确定平面，则第三条直线在这个平面内．

②中可能有直线和平面平行．

③中直线最多可确定3个平面．

④同①.

答案：①④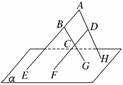

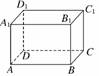
1.如图所示，ABCD－A₁B₁C₁D₁是长方体，O是B₁D₁的中点，

直线A₁C交平面AB₁D_1到于点M，则下列结论正确的是　 (　)

A．A、M、O三点共线

B．A、M、O、A₁不共面

C．A、M、C、O不共面

D．B、B₁、O、M共面

解析：连结A₁C₁，AC，则A₁C₁∥AC，

∴A₁、C₁、C、A四点共面，

∴A₁C⊂平面ACC₁A₁，

∵M∈A₁C，∴M∈平面ACC₁A₁，又M∈平面AB₁D₁，

∴M在平面ACC₁A₁与平面AB₁D₁的交线上，

同理O在平面ACC₁A₁与平面AB₁D₁的交线上，

∴A、M、O三点共线．

答案：A

3．在△ABC中，已知cos(+A)＝，则cos2A的值为________．

解析：cos(+A)＝coscosA－sinsinA

＝(cosA－sinA)＝，

∴cosA－sinA＝＞0.　　　　　　　　　　　　　　　　　　　　　　　　 ①

∴0＜A＜，∴0＜2A＜

①²得1－sin2A＝，∴sin2A＝.

∴cos2A＝＝.

2．(2010·平顶山模拟)在△ABC中，sin²A+cos²B＝1，则cosA+cosB+cosC的最大值为(　)

A.　 　　　B.　　　　 C．1 　　　　D.

解析：由sin²A+cos²B＝1，得sin²A＝sin²B，

∴A＝B，故cosA+cosB+cosC＝2cosA－cos2A

＝－cos²A+2cosA+1.

又0＜A＜，0＜cosA＜1.

∴cosA＝时，有最大值.

答案：D