9．某公司租地建仓库，每月土地占用费y₁与仓库到车站的距离成反比，而每月库存货物的运费y₂与到车站的距离成正比，如果在距离车站10千米处建仓库，这两项费用y₁和y₂分别为2万元和8万元，那么，要使这两项费用之和最小，仓库应建在离车站________千米处．

解析：设仓库建在离车站d千米处，

由已知y₁＝2＝，得k₁＝20，∴y₁＝，

y₂＝8＝k₂·10，得k₂＝，∴y₂＝d，

∴y₁+y₂＝+≥2 ＝8，

当且仅当＝，即d＝5时，费用之和最小．

答案：5

　10．(文)某造纸厂拟建一座平面图形为矩形且面积为162 　　　　　x

平方米的三级污水处理池，池的深度一定(平面图如图所示)，如果池四周围墙建造单价为400元/米，中间两道隔墙建造单价为248元/米，池底建造单价为80元/米²，水池所有墙的厚度忽略不计．

(1)试设计污水处理池的长和宽，使总造价最低，并求出最低总造价；

(2)若由于地形限制，该池的长和宽都不能超过16米，试设计污水池的长和宽，使总造价最低，并求出最低总造价．

解：(1)设污水处理池的宽为x米，则长为米．

则总造价f(x)＝400×(2x+)+248×2x+80×162＝1 296x++12 960

＝1 296(x+)+12 960

≥1 296×2 +12 960＝38 880(元)，

当且仅当x＝(x>0)，

即x＝10时取等号．

∴当长为16.2米，宽为10米时总造价最低，最低总造价为38 880元．

(2)由限制条件知，∴10≤x≤16.

设g(x)＝x+(10≤x≤16)，

由函数性质易知g(x)在上是增函数，

∴当x＝10时(此时＝16)，

g(x)有最小值，即f(x)有最小值

1 296×(10+)+12 960＝38 882(元)．

∴当长为16米，宽为10米时，总造价最低，为38 882元．

(理)为了提高产品的年产量，某企业拟在2010年进行技术改革．经调查测算，产品当年的产量x万件与投入技术改革费用m万元(m≥0)满足x＝3－(k为常数)．如果不搞技术改革，则该产品当年的产量只能是1万件．已知2010年生产该产品的固定投入为8万元，每生产1万件该产品需要再投入16万元．由于市场行情较好，厂家生产的产品均能销售出去．厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金)．

(1)将2010年该产品的利润y万元(利润＝销售金额－生产成本－技术改革费用)表示为技术改革费用m万元的函数；

(2)该企业2010年的技术改革费用投入多少万元时，厂家的利润最大？

解：(1)由题意可知，当m＝0时，x＝1(万件)，

∴1＝3－k，∴k＝2，∴x＝3－，

每件产品的销售价格为1.5×(元)，

∴2010年的利润

y＝x·－(8+16x)－m

＝－[+(m+1)]+29(元)(m≥0)．

(2)∵m≥0，∴+(m+1)≥2＝8，

∴y≤29－8＝21，

当＝m+1，即m＝3，y_max＝21.

∴该企业2010年的技术改革费用投入3万元时，厂家的利润最大．

8.(2010·惠州模拟)某商场中秋前30天月饼销售总量f(t)与时间t(0<t≤30)的关系大致满足f(t)＝t²+10t+16，则该商场前t天平均售出(如前10天的平均售出为)的月饼最少为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．18 　　　　B．27 　　　　　C．20　 　　　D．16

解析：平均销售量y＝＝＝t++10≥18.

当且仅当t＝，即t＝4∈等号成立，即平均销售量的最小值为18.

答案：A

7．已知a、b、c∈(0，+∞)且a+b+c＝1，

求证：(－1)(－1)(－1)≥8.

证明：∵a、b、c∈(0，+∞)且a+b+c＝1，

∴(－1)(－1)(－1)＝

＝≥＝8.

当且仅当a＝b＝c＝时取等号．

6．设a、b是正实数， 以下不等式

①>；②a>|a－b|－b；③a²+b²>4ab－3b²；④ab+>2恒成立的

序号为　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．①③ 　　　　B．①④　　　　 C．②③　 　　　D．②④

解析：∵a、b是正实数，∴①a+b≥2⇒1≥⇒≥.当且仅当a＝b时　　　

取等号，∴①不恒成立；②a+b>|a－b|⇒a>|a－b|－b恒成立；③a²+b²－4ab+3b²＝(a－2b)²≥0，当a＝2b时，取等号，∴③不恒成立；④ab+≥2 ＝2 >2恒成立．

答案：D

5.已知a≥0，b≥0，且a+b＝2，则　　　　　　　 　　　　　　　　　　　　(　)

A．ab≤　 　　　B．ab≥　　　 C．a²+b²≥2 　　　　D．a²+b²≤3

解析：法一：由≥得ab≤()²＝1，又a²+b²≥2ab⇒2(a²+b²)≥(a+b)²⇒a²+b²≥2.

法二：(特值法)取a＝0，b＝2满足a+b＝2，代入选项可排除B、D.又取a＝b＝1满足a+b＝2.但ab＝1，可排除A.

答案：C

4．(2010·太原模拟)若直线ax－by+2＝0(a>0，b>0)和函数f(x)＝a^x+1+1(a>0且a≠1)的图象恒过同一个定点，则当+取最小值时，函数f(x)的解析式是________．

解析：函数f(x)＝a^x+1+1的图象恒过(－1,2)，故a+b＝1，+＝(a+b)(+)＝++≥+.当且仅当b＝a时取等号，将b＝a代入a+b＝1得a＝2－2，故f(x)＝(2－2)^x+1+1.

答案：f(x)＝(2－2)^x+1+1

3．已知不等式(x+y)(+)≥9对任意正实数x，y恒成立，则正实数a的最小值为　 (　)

A．8 　　　B．6　　　 C．4　　 　D．2

解析：(x+y)(+)＝1+a·++a

≥a+1+2 ＝a+2 +1，

当且仅当a·＝等号成立，

所以()²+2+1≥9，

即()²+2－8≥0，得≥2或≤－4(舍)，

所以a≥4，即a的最小值为4.

答案：C

2．(2009·天津高考)设a>0，b>0.若是3^a与3^b的等比中项，则+的最小值为　 (　)

A．8 　　　　　B．4 　　　　　C．1 　　　　　D.

解析：∵是3^a与3^b的等比中项，∴()²＝3^a·3^b.

即3＝3^a+b，∴a+b＝1.

此时+＝+＝2+(+)≥2+2＝4(当且仅当a＝b＝取等号)．

答案：B

1.设x、y均为正实数，且+＝1，则xy的最小值为　　　　　　　　 (　)

A．4　 　　　B．4 　　　　　C．9　　 　D．16

解析：由+＝1可得xy＝8+x+y.

∵x，y均为正实数，

∴xy＝8+x+y≥8+2(当且仅当x＝y时等号成立)，

即xy－2－8≥0，

可解得≥4，即xy≥16，故xy的最小值为16.

答案：D

9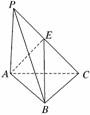．(2010·大连模拟)如图所示，三棱锥P－ABC中，

PA⊥平面ABC，∠BAC＝60°，PA＝AB＝AC＝2，

E是PC的中点．

(1)(文)求证AE与PB是异面直线．

(理)求异面直线AE和PB所成角的余弦值；

(2)求三棱锥A－EBC的体积．

解：(1)(文)证明：假设AE与PB共面，设平面为α，

∵A∈α，B∈α，E∈α，

∴平面α即为平面ABE，

∴P∈平面ABE，

这与P∉平面ABE矛盾，

所以AE与PB是异面直线．

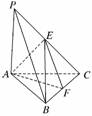
(理)取BC的中点F，连结EF、AF，则EF∥PB，

所以∠AEF或其补角就是异面直线AE和PB所成角．

∵∠BAC＝60°，PA＝AB＝AC＝2，PA⊥平面ABC，

∴AF＝，AE＝，EF＝；

cos∠AEF＝＝，

所以异面直线AE和PB所成角的余弦值为.

(2)因为E是PC中点，所以E到平面ABC的距离为PA＝1，

V_A－EBC＝V_E－ABC＝×(×2×2×)×1＝.