5.已知f(x)在R上是奇函数，且满足f(x+4)＝f(x)，当x∈(0,2)时，f(x)＝2x²，则f(7)＝(　)

A.－2　 　　　B.2　　　　　 C.－98　 　　　　　　D.98

解析：由f(x+4)＝f(x)，得f(7)＝f(3)＝f(－1)，

又f(x)为奇函数，∴f(－1)＝－f(1)，

f(1)＝2×1²＝2，∴f(7)＝－2.故选A.

答案：A

4.已知函数f (x)＝ax⁴+bcosx－x，且f (－3)＝7，则f (3)的值为　　　　　　　　　 (　)

A.1　 　　　B.－7 　　　C.4 　　　　D.－10

解析：设g(x)＝ax⁴+bcosx，则g(x)＝g(－x).由f (－3)＝g(－3)+3，得g(－3)＝f(－3)－3＝4，所以g(3)＝g(－3)＝4，所以f (3)＝g(3)－3＝4－3＝1.

答案：A

3.(2009·浙江高考)若函数f(x)＝x²+(a∈R)，则下列结论正确的是　 　　　　　(　)

A.∀a∈R，f(x) 在(0，+∞)上是增函数

B.∀a∈R，f(x)在(0，+∞)上是减函数

C.∃a∈R，f(x)是偶函数

D.∃a∈R，f(x)是奇函数

解析：当a＝16时，f(x)＝x²+，f′(x)＝2x－，

令f′(x)＞0得x＞2.

∴f(x)在(2，+∞)上是增函数，故A、B错.

当a＝0时，f(x)＝x²是偶函数，故C正确.

D显然错误，故选C.

答案：C

2.(2010·长郡模拟)已知二次函数f(x)＝x²－ax+4，若f(x+1)是偶函数，则实数a的值为(　)

A.－1　　 　B.1 　　C.－2　 　　　　D.2

解析：∵f(x)＝x²－ax+4，

∴f(x+1)＝(x+1)²－a(x+1)+4

＝x²+2x+1－ax－a+4

＝x²+(2－a)x+5－a，

f(1－x)＝(1－x)²－a(1－x)+4

＝x²－2x+1－a+ax+4

＝x²+(a－2)x+5－a.

∵f(x+1)是偶函数，

∴f(x+1)＝f(－x+1)，

∴a－2＝2－a，即a＝2.

答案：D

1.已知y＝f(x)是定义在R上的奇函数，则下列函数中为奇函数的是　　　　　　 (　)

①y＝f(|x|)；②y＝f(－x)；③y＝xf(x)；④y＝f(x)+x.

A.①③　 　　　　　　B.②③

C.①④　 　　　　　　D.②④

解析：由奇函数的定义验证可知②④正确，选D.

答案：D

12．为了保证信息安全传输，有一种称为秘密密钥密码系统，其加密、解密原理如下图：

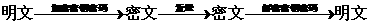
现在加密密钥为y＝log_a(x+2)，如上所示，明文“6”通过加密后得到密文“3”，再发送，接受方通过解密密钥解密得到明文“6”．问：若接受方接到密文为“4”，则解密后得到明文为　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．12　　　　　 　B．13 　　　　　C．14 　　　　　D．15

解析：∵log_a(6+2)＝3，∴a＝2，

即加密密钥为y＝log₂(x+2)，

当接到的密文为4时，即log₂(x+2)＝4，∴x+2＝2⁴，

∴x＝14.

答案：C

11．“因为指数函数y＝a^x是增函数(大前提)，而y＝()^x是指数函数(小前提)，所以y＝()^x是增函数(结论)”，上面推理的错误是　　　　　　　　　　　　　　 (　)

A．大前提错导致结论错

B．小前提错导致结论错

C．推理形式错导致结论错

D．大前提和小前提错都导致结论错

解析：y＝a^x是增函数这个大前提是错误的，从而导致结论错．

答案：A

10．下面几种推理过程是演绎推理的是　　　　　　　　　　　　　　　　　　 (　)

A．两条直线平行，同旁内角互补，由此若∠A，∠B是两条平行直线被第三条直线所截得的同旁内角，则∠A+∠B＝180°

B．某校高三(1)班有55人，高三(2)班有54人，高三(3)班有52人，由此得出高三所有班人数超过50人

C．由平面三角形的性质，推测空间四面体的性质

D．在数列{a_n}中，a₁＝1，a_n＝(a_n－1+)(n≥2)，由此归纳出{a_n}的通项公式

解析：两条直线平行，同旁内角互补┄┄┄┄┄┄大前提

∠A，∠B是两条平行直线被第三条直┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄小前提

∠A+∠B＝180°┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄结论

故A是演绎推理，而B、D是归纳推理，C是类比推理．

答案：A

9.(2009·广东高考)广州2010年亚运会火炬传递在A，B，C，D，E五个城市之间进行，各城市之间的路线距离(单位：百公里)见下表．若以A为起点，E为终点，每个城市经过且只经过一次，那么火炬传递的最短路线距离是　　　　　　　　　　　 (　)

A.20.6　 　　　B．21　　 　　　C．22　　　　 　D．23

解析：首先以A为起点，E为终点，每个城市经过且只经过1次的可能性有A种，即ABCDE，ABDCE，ACBDE，ACDBE，ADBCE，ADCBE，分别计算得ACDBE最短，且最短距离为21.

答案：B

8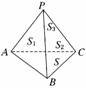．在△ABC中，射影定理可以表示为a＝bcosC+ccosB，其中a，b，c依次为角A、B、C的对边，类比以上定理，给出空间四面体性质的猜想．

解：如图，在四面体P－ABC中，S₁、S₂、S₃、S分别表

示△PAB、△PBC、△PCA、△ABC的面积，α、β、γ依

次表示面PAB、面PBC、面PCA与底面ABC所成角的大

小，我们猜想将射影定理类比推理到三维空间，其表现形式应为S＝S₁cosα+S₂cosβ+S₃cosγ.