2.下列各组函数中，表示同一函数的是　　　　　　　　　　　　　　　　　 　(　)

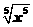A.y＝与y＝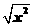

B.y＝lne^x与y＝e^lnx

C.y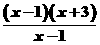＝与y＝x+3

D.y＝x⁰与y＝

解析：对于命题A，对应关系不同；对于命题B，定义域不同；对于命题C，定义域不同；对于命题D，y＝x⁰(x≠0)与y＝　 (x≠0)完全相同.

答案：D

1.设f：x→x²是从集合A到集合B的映射，如果B＝{1,2}，则A∩B为　　　　　　 (　)

A.∅　 　　B.{1}　　　 C.∅或{2} 　　　　D.∅或{1}

解析：由已知x²＝1或x²＝2，解之得x＝±1或x＝±.若1∈A，则A∩B＝{1}，若1∉A，则A∩B＝∅.故A∩B＝∅或{1}.

答案：D

12.(文)某城市在发展过程中，交通状况逐渐受到大家更多的关注，据有关统计数据显示，从上午6点到中午12点，车辆通过该市某一路段的用时y(分钟)与车辆进入该路段的时刻t之间的关系可近似地用如下函数给出：

y＝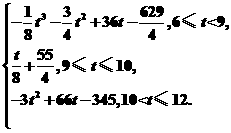

求从上午6点到中午12点，通过该路段用时最多的时刻.

解：(1)当6≤t＜9时，

y′＝－t²－t+36＝－(t²+4t－96)

＝－(t+12)(t－8).

令y′＝0，得t＝－12或t＝8.

∴当t＝8时，y有最大值.

y_max＝18.75(分钟).

(2)当9≤t≤10时，y＝t+是增函数，

∴当t＝10时，y_max＝15(分钟).

(3)当10＜t≤12时，y＝－3(t－11)²+18，

∴当t＝11时，y_max＝18(分钟).

综上所述，上午8时，通过该路段用时最多，为18.75分钟.

(理)某厂生产某种零件，每个零件的成本为40元，出厂单价定为60元，该厂为了鼓励销售商订购，决定每一次订购量超过100个时，每多订购一个，多订购的全部零件的出厂单价就降0.02元，但实际出厂单价不能低于51元.

(1)当一次订购量为多少个时，零件的实际出厂单价恰降为51元？

(2)设一次订购量为x个，零件的实际出厂单价为P元，写出函数P＝f(x)的表达式.

(3)当销售商一次订购500个零件时，该厂获得的利润是多少元？如果订购1000个，利 润又是多少元？

解：(1)设每个零件的实际出厂价格恰好降为51元时，一次订购量为x₀个，则x₀＝100+＝550.因此，当一次订购量为550个时，每个零件的实际出厂价恰好降为51元.

(2)当0＜x≤100时，P＝60；

当100＜x＜550时，P＝60－0.02(x－100)＝62－；

当x≥550时，P＝51.

所以P＝f(x)＝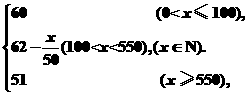

　(3)设销售商的一次订购量为x个时，工厂获得的利润为L元，则

L＝(P－40)x＝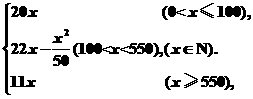

当x＝500时，L＝6000；

当x＝1000时，L＝11000.

因此，当销售商一次订购500个零件时，该厂获得的利润是6000元；如果订购1000个，利润是11000元.

11.(2010·沈阳模拟)沪杭高速公路全长166千米.假设某汽车从上海莘庄镇进入该高速公路后以不低于60千米/时且不高于120千米/时的速度匀速行驶到杭州.已知该汽车每小时的运输成本y(以元为单元)由可变部分和固定部分组成：可变部分与速度v(千米/时)的平方成正比，比例系数为0.02；固定部分为200元.

(1)把全程运输成本y(元)表示为速度v(千米/时)的函数，并指出这个函数的定义域；

(2)汽车应以多大速度行驶才能使全程运输成本最小？最小运输成本为多少元？

解：(1)依题意得：y＝(200+0.02v²)×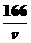

＝166(0.02v+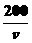)(60≤v≤120).

(2)y＝166(0.02v+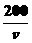)≥166×2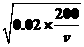

＝664(元).

当且仅当0.02v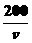＝即v＝100 千米/时时取等号.

答：当速度为100 千米/时时，最小的运输成本为664元.

10.鲁能泰山足球俱乐部准备为救助失学儿童在山东省体育中心体育场举行一场足球义赛，预计卖出门票2.4万张，票价有3元、5元和8元三种，且票价3元和5元的张数的积为0.6万张.设x是门票的总收入，经预算，扣除其他各项开支后，该俱乐部的纯收入为函数y＝lg2^x，则这三种门票的张数分别为　　　　　万张时可以为失学儿童募捐的纯收入最大.

解析：该函数模型y＝lg 2^x已给定，因而只需要将条件信息提取出来，按实际情况代入，应用于函数即可解决问题.

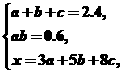设3元、5元、8元门票的张数分别为a、b、c，则

　　　　　　　　　　　　　　　　　　　　 ①

　　　　　　　　　　　　　　　　　　　　 ②

　　　 　　　　　　　　　　　　　　　　③

①代入③有x＝19.2－(5a+3b)≤19.2－2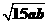

＝13.2(万元)，

当且仅当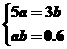 时等号成立，

解得a＝0.6，b＝1，所以c＝0.8.

由于y＝lg 2^x为增函数，即此时y也恰有最大值.

故三种门票的张数分别为0.6、1、0.8万张时可以为失学儿童募捐的纯收入最大.

答案：0.6、1、0.8

9.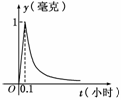为了预防流感，某学校对教室用药熏消毒法进行消毒，

已知药物释放过程中，室内每立方米空气中的含药量

y(毫克)与时间t(小时)成正比；药物释放完毕后，y与t

的函数关系式为y＝()^t－a(a为常数)，如图所示，根

据图中提供的信息，回答下列问题：

(1)从药物释放开始，每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系为　　　　　　　　　　　　 ；

(2)据测定，当空气中每立方米的含药量降低到0.25毫克以下时，学生方可进教室，那么从药物释放开始，至少需要经过　　小时后，学生才能回到教室.

解析：(1)设y＝kt，由图象知y＝kx过点(0.1,1)，则

1＝k×0.1，k＝10，∴y＝10t(0≤t≤0.1)；

由y＝()^t－a过点(0.1,1)得1＝()^0.1－a，

a＝0.1，∴y＝()^t－0.1(t＞0.1).

(2)由()^t－0.1≤0.25＝得t≥0.6，故至少需经过0.6小时.

答案：(1)y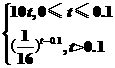＝ (2)0.6

8.某市2008年新建住房100万平方米，其中有25万平方米经济适用房，有关部门计划以后每年新建住房面积比上一年增加5%，其中经济适用房每年增加10万平方米.按照此计划，当年建造的经济适用房面积首次超过该年新建住房面积一半的年份是(参考数据：1.05²＝1.10,1.05³＝1.16,1.05⁴＝1.22,1.05⁵＝1.28)　　　　　　　　　　　 (　)

A.2010年 　　　B.2011年　　 　C.2012年　 　　　D.2013年

解析：设第n年新建住房面积为a_n＝100(1+5%)ⁿ，经济适用房面积为b_n＝25+10n，由2b_n＞a_n得：2(25+10n)＞100(1+5%)ⁿ，利用已知条件解得n＞3，所以在2012年时满足题意.故选C.

答案：C

7.手机的价格不断降低，若每隔半年其价格降低，则现在价格为2 560元的手机，两年后价格可降为　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.900元　 　　　B.810元　　　　 C.1440元 　　　　D.160元

解析：半年降价一次，则两年后降价四次，其价格降为2560×⁴＝810.

答案：B

6.某工厂生产某种产品固定成本为2 000万元，并且每生产一单位产品，成本增加10万元.又知总收入K是单位产品数Q的函数，K(Q)＝40Q－Q²，则总利润L(Q)的最大值是　　　.

解析：总利润L(Q)＝40Q－Q²－10Q－2 000

＝－(Q－300)²+2 500.

故当Q＝300时，总利润最大值为2 500万元.

答案：2 500万元

5.某公司在甲、乙两地销售一种品牌车，利润(单位：万元)分别为L₁＝5.06x－0.15x²和L₂＝2x，其中x为销售量(单位：辆).若该公司在这两地共销售15辆车，则能获得最大利润为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.45.606　 　　B.45.6 　　　C.45.56　 　　　　　D.45.51

解析：依题意可设甲销售x辆，则乙销售(15－x)辆，

∴总利润S＝5.06x－0.15x²+2(15－x)

＝－0.15x²+3.06x+30(x≥0).

∴当x＝10时，S_max＝45.6(万元).

答案：B