10．(2010·三亚模拟)在长为1的线段上任取两点，则这两点之间的距离小于的概率为(　)

A.　　　　　 　B.　　　　　　　　　　 C.　 　　　　　　　　　　D.

解析：两点设为a，b，则0≤a≤1,0≤b≤1，两点之间的距离小于，则|a－b|<，画出可行域，为图中阴影部分，面积为，概率为.

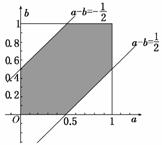
答案：C

9．抛掷两个骰子，至少有一个4点或5点出现时，就说这次实验成功，则在10次实验中，成功次数ξ的期望是　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　B.　　　　　　　 C.　 　　　　　　　　　D.

解析：由题意一次试验成功的概率为1－×＝，10次试验为10次独立重复试验，则成功次数ξ-B，所以E(ξ)＝.

答案：C

8．某班班会准备从甲、乙等7名学生中选派4名学生发言，要求甲、乙两人至少有一人参加．当甲乙同时参加时，他们两人的发言不能相邻．那么不同的发言顺序的种数为　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　(　)

A．360　 　　　　　　　B．520 　　　　　　　　C．600　 　　　　　　　　D．720

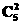
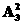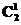
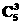
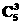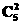
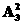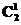
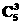
解析：若甲乙同时参加，可以先从剩余的5人中选出2人，先排此两人，再将甲乙两人插入其中即可，则共有种不同的发言顺序；若甲乙两人只有一人参加，则共有种不同的发言顺序，综合可得不同的种发言顺序为+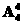＝600种．

答案：C

7．在某地的奥运火炬传递活动中，有编号为1,2,3，…，18的18名火炬手．若从中任选3人，则选出的火炬手的编号能组成以3为公差的等差数列的概率为　　 (　)

A. 　　　　　　　　B.　　　　　　　　　　 C. 　　　　　　　　　D.

解析：基本事件总数n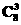＝，以1为首项3为公差的等差数列，共有6项，符合题意的火炬手有4种选法；同理以2为首项3为公差的等差数列，以3为首项3为公差的等差数列，符合题意的选法分别有4种，故所求概率P＝＝.

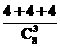答案：B

6．已知随机变量ξ服从正态分布N(4,6²)，P(ξ≤5)＝0.89，则P(ξ≤3)＝　　　　　 (　)

A．0.89　 　　　　　B．0.22 　　　　C．0.11　 　　　　　　　D．0.78

解析：由题意知正态分布图象关于直线x＝4对称，故由P(ξ≤5)＝0.89⇒P(4≤ξ≤5)＝0.89－0.5＝0.39，因此P(3≤ξ≤4)＝0.39，故有P(ξ≤3)＝0.5－P(3≤ξ≤4)＝0.5－0.39＝0.11.

答案：C

5．设随机变量ξ的分布列为P(ξ＝k)＝p^k(1－p)^1－k(k＝0,1)，则E(ξ)，D(ξ)的值分别是(　)

A．0和1 　　　　　B．p和p²C．p和1－p 　　　　　D．p和(1－p)·p

解析：ξ的分布列表为：

知ξ服从两点分布．

∴E(ξ)＝p，D(ξ)＝1×p(1－p)＝p(1－p)．

答案：D

4．在面积为S的△ABC的边AB上任取一点P，则△PBC的面积大于的概率是 (　)

A. 　　　　　　　B.　　　　　　　　　 C.　 　　　　　　　　　D.

解析：由已知可设△ABC的边AB上的高为h.

则S＝|AB|·h，S_△PBC＝|PB|·h，

所以S_△PBC＝·S>，

又|PB|>|AB|的概率为；

故S_△PBC>的概率为.

答案：C

3．(2010·安顺模拟)某班级要从5名男生、3名女生中选派4人参加某次社区服务，如果要求至少有一名女生，那么选派的4人中恰好有2名女生的概率为　　　　　　 (　)

A. 　　　　　　　　　B.　　　　　　　　　 C. 　　　　　　　　　　　D.

解析：由已知易知至少有一名女生的情况共有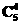－种，而恰有2名女生的情况共有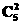种可能，

故其概率为＝.

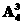答案：D

2．在(1+x+x²)(1－x)¹⁰的展开式中，含x⁴项的系数是　　　　　　　　　　　　 (　)

A．135 　　　　　　B．－135 　　　　　　　C．375　 　　　　　　　　D．－117

解析：(1+x+x²)(1－x)¹⁰＝(1－x³)(1－x)⁹，且(1－x)⁹的展开式的通项是T_r+1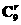＝·(－x)^r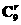＝·(－1)^r·x^r，因此(1+x+x²)(1－x)¹⁰的展开式中，含x⁴项的系数等于1×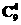·(－1)⁴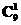－·(－1)¹＝135.

答案：A

1．A、B、C、D、E五人排一个5天的值日表，每天由一人值日，每人可以值多天或不值，但相邻的两天不能由同一人值，那么值日表的排法种数为　　　　　　 (　)

A．120　　　　B．324 　　　　　　　　　　C．720　 　　　　　　D．1 280

解析：第一天有5种排法，以后各天都有4种排法，故总排法为N＝5×4×4×4×4＝1 280种．

答案：D