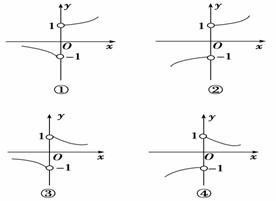
4．已知函数f(x)＝4－x²，g(x)是定义在(－∞，0)∪(0，+∞)上的奇函数，当x>0时，g(x)＝log₂x，则函数y＝f(x)·g(x)的大致图象为__________．

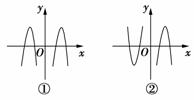
解析：f(x)为偶函数，g(x)是奇函数，所以f(x)·g(x)为奇函数，图象关于原点对称，当x→+∞时，f(x)→－∞，g(x)→+∞，所以f(x)·g(x)→－∞答案：②

3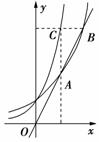．如图，过原点O的直线与函数y＝2^x的图象交于A，B两点，过B作y轴的垂线交函数y＝4^x的图象于点C，若AC平行于y轴，则点A的坐标是__________．

解析：设C(a,4^a)，所以A(a,2^a)，B(2a,4^a)，又O，A，B三点共线，所以＝，故4^a＝2×2^a，所以2^a＝0(舍去)或2^a＝2，即a＝1，所以点A的坐标是(1,2)．答案：(1,2)

2．家电下乡政策是应对金融危机、积极扩大内需的重要举措．我市某家电制造集团为尽快实现家电下乡提出四种运输方案，据预测，这四种方案均能在规定时间T内完成预期的运输任务Q₀，各种方案的运输总量Q与时间t的函数关系如下图所示．在这四种方案中，运输效率(单位时间的运输量)逐步提高的是　　

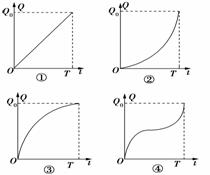
解析：运输效率是运输总量Q与时间t的函数的导数，几何意义为图象的切线，切线斜率的增长表明运输效率的提高，从图形看，②正确．

答案：②

1.(2010年合肥市高三质检)函数f(x)＝ln的图象只可能是__________．

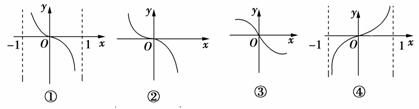
解析：本题中f(x)的定义域为{x|－1<x<1}，从而排除②③选项．又由于u(x)＝－1+在定义域{x|－1<x<1}内是减函数，而g(x)＝lnx在定义域(0，+∞)内是增函数，从而f(x)＝ln＝ln(－1+)在定义域{x|－1<x<1}是减函数．

答案：①

6．已知函数f(x)＝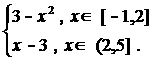

(1)画出f(x)的图象；(2)写出f(x)的单调递增区间．

解：(1)函数f(x)的图象如图所示．,

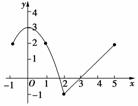
(2)由图象可知，函数f(x)的单调递增区间为[-1,0]，[2,5]．

B组

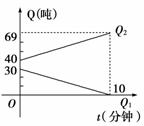
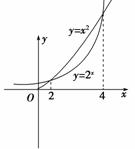
5．(原创题)已知当x≥0时，函数y＝x²与函数y＝2x的图象如图所示，则当x≤0时，不等式2^x·x²≥1的解集是__________．

解析：在2^x·x²≥1中，令x＝－t，由x≤0得t≥0，

∴2^－t·(－t)²≥1，即t²≥2^t，由所给图象得2≤t≤4，

∴2≤－x≤4，解得－4≤x≤－2.

答案：－4≤x≤－2

4．(2009年高考安徽卷改编)设a<b，函数y＝(x－a)²(x－b)的图象可能是_____．

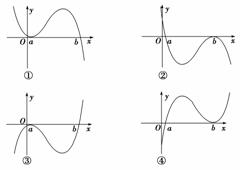
解析：∵x>b时，y>0.由数轴穿根法，从右上向左下穿，奇次穿偶次不穿可知，只有③正确．答案：③

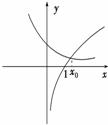
3．已知函数f(x)＝()^x－log₃x，若x₀是方程f(x)＝0的解，且0<x₁<x₀，则f(x₁)的值为__________(正负情况)．

解析：分别作y＝()^x与y＝log₃x的图象，如图可知，当0<x₁<x₀时，()^x1>log₃x₁，

∴f(x₁)>0.答案：正值

2．(2010年济南市高三模拟考试)函数y＝·a^x(a>1)的图象的基本形状是_____．

解析：先去绝对值将已知函数写成分段函数形式，再作图象即可，函数解析式：y＝，由指数函数图象易知①正确．

答案：①

1．命题甲：已知函数f(x)满足f(1+x)＝f(1－x)，则f(x)的图象关于直线x＝1对称．命题乙：函数f(1+x)与函数f(1－x)的图象关于直线x＝1对称．则甲、乙命题正确的是__________．

解析：可举实例说明如f(x)＝2^x，依次作出函数f(1+x)与函数f(1－x)的图象判断．答案：甲