2．(2010年广东广州质检)下列图象中，表示y＝x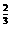的是________．

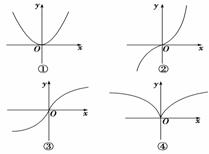
解析：y＝x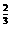＝是偶函数，∴排除②、③，当x>1时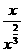，＝x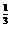>1，∴x>x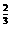，∴排除①.答案：④

1．若a>1且0<b<1，则不等式alog_b(x－3)>1的解集为________．

解析：∵a>1,0<b<1，∴alog_b(x－3)>1⇔log_b(x－3)>0⇔log_b(x－3)>log_b1⇔0<x－3<1⇔3<x<4.答案：{x|3<x<4}

12．设函数f(x)＝(x∈R，且a≠0，x≠)．(1)若a＝，b＝－，指出f(x)与g(x)＝的图象变换关系以及函数f(x)的图象的对称中心；(2)证明：若ab+1≠0，则f(x)的图象必关于直线y＝x对称．

解：(1)a＝，b＝－，f(x)＝＝＝2+，

∴f(x)的图象可由g(x)的图象沿x轴右移2个单位，再沿y轴上移2个单位得到，f(x)的图象的对称中心为点(2,2)．

(2)证明：设P(x₀，y₀)为f(x)图象上任一点，则y₀＝，P(x₀，y₀)关于y＝x的对称点为P′(y₀，x₀)．由y₀＝得x₀＝.∴P′(y₀，x₀)也在f(x)的图象上．故f(x)的图象关于直线y＝x对称.

11．已知函数f(x)＝－(a>0且a≠1)．(1)证明：函数y＝f(x)的图象关于点(，－)对称；(2)求f(－2)+f(－1)+f(0)+f(1)+f(2)+f(3)的值．

解：(1)证明：函数f(x)的定义域为R，任取一点(x，y)，它关于点(，－)对称的点的坐标为(1－x，－1－y)．由已知，y＝－，则－1－y＝－1+＝－.,f(1－x)＝－＝－＝－＝－.

∴－1－y＝f(1－x)．即函数y＝f(x)的图象关于点(，－)对称．

(2)由(1)有－1－f(x)＝f(1－x)．即f(x)+f(1－x)＝－1.

∴f(－2)+f(3)＝－1，f(－1)+f(2)＝－1，f(0)+f(1)＝－1.

则f(－2)+f(－1)+f(0)+f(1)+f(2)+f(3)＝－3.

10．作下列函数的图象：

(1)y＝；(2)y＝|x－2|(x+1)；(3)y＝；(4)y＝|log₂x－1|；(5)y＝2^|x_－^1|.

解：(1)定义域{x|x∈R且x≠±1}，且函数是偶函数．又当x≥0且x≠1时，y＝.先作函数y＝的图象，并将图象向右平移1个单位，得到函数y＝(x≥0且x≠1)的图象(如图(a)所示)．

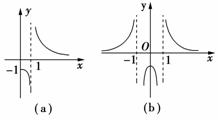
又函数是偶函数，作关于y轴对称图象，得y＝的图象(如图(b)所示)．

(2)函数式可化为y＝其图象如图①所示．

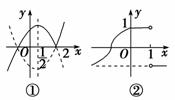
(3)函数式化为y＝其图象如图②所示．

(4)先作出y＝log2x的图象，再将其图象向下平移1个单位长度，保留x轴上方的部分，将x轴下方的图象翻折到x轴上方，即得y＝|log2x－1|的图象，如图③所示．

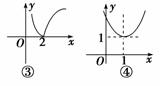
(5)先作出y＝2^x的图象，再将其图象在y轴左边的部分去掉，并作出y轴右边的图象关于y轴对称的图象，即得y＝2^|x|的图象，再将y＝2^|x|的图象向右平移1个单位长度，即得y＝2^|x－1|的图象，如图④所示．

9．(2010年安徽合肥模拟)已知函数图象C′与C：y(x+a+1)＝ax+a²+1关于直线y＝x对称，且图象C′关于点(2，－3)对称，则a的值为__________．

解析：∵C′与C：y(x+a+1)＝ax+a²+1关于直线y＝x对称，

∴C′为x(y+a+1)＝ay+a²+1.整理得，y+1+a＝.

∵C′关于点(2，－3)对称，∴a＝2.答案：2

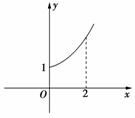
8．(2009年高考福建卷改编)定义在R上的偶函数f(x)的部分图象如图所示，则在(－2,0)上，下列函数中与f(x)的单调性不同的是　　

①y＝x²+1

②y＝|x|+1

③y＝

④y＝

解析：∵f(x)为偶函数，由图象知，f(x)在(－2,0)上为减函数，而y＝x³+1在(－∞，0)上为增函数．答案：③

7．函数y＝x(m，n∈Z，m≠0，|m|，|n|互质)图象如图所示，则下列结论正确的是__________．

①mn>0，m，n均为奇数

②mn<0，m，n一奇一偶

③mn<0，m，n均为奇数

④mn>0，m，n一奇一偶

解析：由于幂函数在第一象限的图象趋势表明函数在(0，+∞)上单调递减，此时只需保证<0，即mn<0，有y＝x＝x－；同时函数只在第一象限有图象，则函数的定义域为(0，+∞)，此时|n|定为偶数，n即为偶数，由于两个数互质，则m定为奇数．答案：②

6．已知函数y＝f(x)(x∈R)满足f(x+2)＝f(x)，且x∈(－1,1]时，f(x)＝|x|，则y＝f(x)与y＝log₇x的交点的个数为__________．

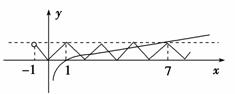
解析：由f(x+2)＝f(x)知函数y＝f(x)为周期为2的周期函数，作图．

答案：6

5．某加油机接到指令，给附近空中一运输机加油．运输机的余油量为Q₁(吨)，加油机加油箱内余油Q₂(吨)，加油时间为t分钟，Q₁、Q₂与时间t的函数关系式的图象如右图．若运输机加完油后以原来的速度飞行需11小时到达目的地，问运输机的油料是否够用？________.

解析：加油时间10分钟，Q₁由30减小为0.Q₂由40增加到69，因而10分钟时间内运输机用油1吨．以后的11小时需用油66吨．因69>66，故运输机的油料够用．答案：够用