4．(2009年高考福建卷改编)设m，n是平面α内的两条不同直线；l₁，l₂是平面β内的两条相交直线，则α∥β的一个充分而不必要条件是________．

①m∥β且l₁∥α　②m∥l₁且n∥l₂ ③m∥β且n∥β 　　④m∥β且n∥l₂

解析：∵m∥l₁，且n∥l₂，又l₁与l₂是平面β内的两条相交直线，

∴α∥β，而当α∥β时不一定推出m∥l₁且n∥l₂，可能异面．答案： ②

3．(2010年苏北四市调研)给出下列关于互不相同的直线m、l、n和平面α、β的四个命题：

①若m⊂α，l∩α＝A，点A∉m, 则l与m不共面；

②若m、l是异面直线，l∥α，m∥α，且n⊥l，n⊥m，则n⊥α；

③若l∥α，m∥β，α∥β，则l∥m；

④若l⊂α，m⊂α，l∩m＝A，l∥β，m∥β，则α∥β.

其中为真命题的是________．

解析：③中若l⊂β，m⊂α，α∥β⇒l∥m或l，m异面，所以②错误．而其它命题都正确．答案：①②④

2．已知m、n是不同的直线，α、β是不重合的平面，给出下列命题：

①若m∥α，则m平行于平面α内的无数条直线；

②若α∥β，m⊂α，n⊂β，则m∥n；

③若m⊥α，n⊥β，m∥n，则α∥β；

④若α∥β，m⊂α，则m∥β.

其中，真命题的序号是________．(写出所有真命题的序号)

解析：②中α∥β，m⊂α，n⊂β⇒m∥n或m，n异面，所以②错误．而其它命题都正确．答案：①③④

1．已知m、n是两条不同直线，α，β是两个不同平面，下列命题中的真命题是_．

①如果m⊂α，n⊂β，m∥n，那么α∥β

②如果m⊂α，n⊂β，α∥β，那么m∥n

③如果m⊂α，n⊂β，α∥β且m，n共面，那么m∥n

④如果m∥n，m⊥α，n⊥β，那么α⊥β

解析：m⊂α，n⊂β，α∥β⇒m，n没有公共点．又m，n共面，

所以m∥n.答案：③

4．已知函数y＝f(x)与y＝e^x互为反函数，函数y＝g(x)的图象与y＝f(x)的图象关于x轴对称，若g(a)＝1，则实数a的值为________．

解析：由y＝f(x)与y＝e^x互为反函数，得f(x)＝lnx，因为y＝g(x)的图象与y＝f(x)的图象关于x轴对称，故有g(x)＝－lnx，g(a)＝1⇒lna＝－1，所以a＝.

3．(2010年枣庄第一次质检)对任意实数a、b，定义运算“*”如下：

a*b＝，则函数f(x)＝log(3x－2)*log₂x的值域为________．

解析：在同一直角坐标系中画出y＝log(3x－2)和y＝log₂x两个函数的图象，

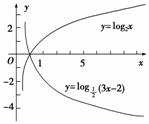
由图象可得

f(x)＝，值域为(－∞，0]．答案：(－∞，0]

2．(2010年安徽黄山质检)对于函数f(x)＝lgx定义域中任意x₁，x₂(x₁≠x₂)有如下结论：①f(x₁+x₂)＝f(x₁)+f(x₂)；②f(x₁·x₂)＝f(x₁)+f(x₂)；③>0；④f()<.上述结论中正确结论的序号是________．

解析：由运算律f(x₁)+f(x₂)＝lgx₁+lgx₂＝lgx₁x₂＝f(x₁x₂)，所以②对；因为f(x)是定义域内的增函数，所以③正确；f()＝lg，＝＝lg，∵≥，且x₁≠x₂，∴lg>lg，所以④错误．

答案：②③

1．(2009年高考北京卷改编)为了得到函数y＝lg的图象，只需把函数y＝lgx的图象上所有的点________．

解析：∵y＝lg＝lg(x+3)－1，∴将y＝lgx的图象上的点向左平移3个单位长度得到y＝lg(x+3)的图象，再将y＝lg(x+3)的图象上的点向下平移1个单位长度得到y＝lg(x+3)－1的图象．

答案：向左平移3个单位长度，再向下平移1个单位长度

6．若f(x)＝x²－x+b，且f(log₂a)＝b，log₂f(a)＝2(a>0且a≠1)．(1)求f(log₂x)的最小值及相应x的值；(2)若f(log₂x)>f(1)且log₂f(x)<f(1)，求x的取值范围．

解：(1)∵f(x)＝x²－x+b，∴f(log₂a)＝(log₂a)²－log₂a+b＝b，∴log₂a＝1，∴a＝2.又∵log₂f(a)＝2，∴f(a)＝4.∴a²－a+b＝4，∴b＝2.∴f(x)＝x²－x+2.

∴f(log₂x)＝(log₂x)²－log₂x+2＝(log₂x－)²+.

∴当log₂x＝，即x＝时，f(log₂x)有最小值.

(2)由题意知∴

∴∴0<x<1.

B组

5．(原创题)已知函数f(x)＝alog₂x+blog₃x+2，且f()＝4，则f(2010)的值为_．

解析：设F(x)＝f(x)－2，即F(x)＝alog₂x+blog₃x，则F()＝alog₂+blog₃＝－(alog₂x+blog₃x)＝－F(x)，∴F(2010)＝－F()＝－[f()－2]＝－2，

即f(2010)－2＝－2，故f(2010)＝0.答案：0