8．下列四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥面MNP的图形的序号是________(写出所有符合要求的图形序号)．

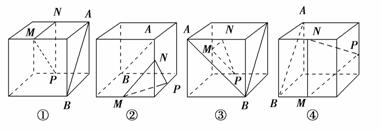
解析：①∵面AB∥面MNP，∴AB∥面MNP.

②若下底面中心为O，易知NO∥AB，NO⊄面MNP，∴AB与面MNP不平行．

③易知AB∥MP，∴AB∥面MNP.

④易知存在一直线MC∥AB，且MC⊄平面MNP，∴AB与面MNP不平行．

答案：①③

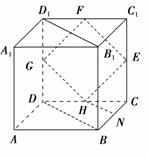
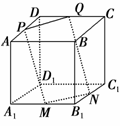
7．如图，ABCD－A₁B₁C₁D₁是棱长为a的正方体，M、N分别是下底面的棱A₁B₁、B₁C₁的中点，P是上底面的棱AD上的一点，AP＝，过P、M、N的平面交上底面于PQ，Q在CD上，则PQ＝______.

答案：a

6．设m、n是异面直线，则(1)一定存在平面α，使m⊂α且n∥α；(2)一定存在平面α，使m⊂α且n⊥α；(3)一定存在平面γ，使m、n到γ的距离相等；(4)一定存在无数对平面α与β，使m⊂α，n⊂β，且α∥β.上述4个命题中正确命题的序号为________．

解析：(1)成立；(2)不成立，m、n不一定垂直；(3)过m、n公垂线段中点分别作m、n的平行线所确定平面到m、n距离就相等，(3)正确；满足条件的平面只有一对，(4)错．答案：(1)(3)

5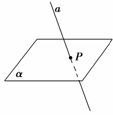．(2010年广东深圳模拟)若a不平行于平面α，且a⊄α，则下列结论成立的是________．

①α内的所有直线与a异面

②α内与a平行的直线不存在

③α内存在唯一的直线与a平行

④α内的直线与a都相交

解析：由题设知，a和α相交，设a∩α＝P，如图，在α内过点P的直线与a共面，①错；在α内不过点P的直线与a异面，④错；(反证)假设α内直线b∥a，∵a⊄α，∴a∥α，与已知矛盾，③错．答案：②

4．设l₁，l₂是两条直线，α，β是两个平面，A为一点，下列命题中正确的命题是________．

①若l₁⊂α，l₂∩α＝A，则l₁与l₂必为异面直线

②若α⊥β，l₁⊂α，则l₁⊥β

③l₁⊂α，l₂⊂β，l₁∥β，l₂∥α，则α∥β

④若l₁∥α，l₂∥l₁，则l₂∥α或l₂⊂α

解析：①错，两直线可相交于点A；②错，不符合面面垂直的性质定理的条件；③错，不符合面面平行的判定定理条件；④正确，空间想象即可．答案：④

3．已知m，n是平面α外的两条直线，且m∥n，则“m∥α”是“n∥α”的________条件．

解析：由于直线m，n在平面外，且m∥n，故若m∥α，则必有n∥α，反之也成立．答案：充要

2．已知m，n是两条不同的直线，α，β是两个不同的平面，有下列4个命题：

①若m∥n，n⊂α，则m∥α；

②若m⊥n，m⊥α，n⊄α，则n∥α；

③若α⊥β，m⊥α，n⊥β，则m⊥n；

④若m，n是异面直线，m⊂α，n⊂β，m∥β，则n∥α.其中正确的命题有_．

解析：对于①，m有可能也在α上，因此命题不成立；对于②，过直线n作垂直于m的平面β，由m⊥α，n⊄α可知β与α平行，于是必有n与α平行，因此命题成立；对于③，由条件易知m平行于β或在β上，n平行于α或在α上，因此必有m⊥n；对于④，取正方体中两异面的棱及分别经过此两棱的不平行的正方体的两个面即可判断命题不成立．综上可知②③正确．答案：②③

1．已知m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题正确的是________．

①若α⊥γ，α⊥β，则γ∥β　 ②若m∥n，m⊂α，n⊂β，则α∥β

③若m∥n，m∥α，则n∥α　 ④若n⊥α，n⊥β，则α∥β

解析：①错，两平面也可相交；②错，不符合面面平行的判定定理条件，需两平面内有两条相交直线互相平行；③错，直线n不一定在平面内；④由空间想象知垂直于同一直线的两平面平行，命题正确．答案：④

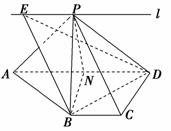
6．如图，ABCD为直角梯形，∠C＝∠CDA＝90°，AD＝2BC＝2CD，P为平面ABCD外一点，且PB⊥BD.

(1)求证：PA⊥BD；

(2)若PC与CD不垂直，求证：PA≠PD；

(3)若直线l过点P，且直线l∥直线BC，试在直线l上找一点E，使得直线PC∥平面EBD.

解：(1)证明：∵ABCD为直角梯形，AD＝AB＝BD，

∴AB⊥BD，PB⊥BD，AB∩PB＝B，

AB，PB⊂平面PAB，BD⊥平面PAB，

PA⊂平面PAB，∴PA⊥BD.

(2)证明：假设PA＝PD，取AD中点N，连结PN，BN，则PN⊥AD，BN⊥AD，

AD⊥平面PNB，得PB⊥AD，

又PB⊥BD，得PB⊥平面ABCD，

∴PB⊥CD.

又∵BC⊥CD，∴CD⊥平面PBC，

∴CD⊥PC，与已知条件PC与CD不垂直矛盾．

∴PA≠PD.

(3)在l上取一点E，使PE＝BC，连结BE，DE，

∵PE∥BC，∴四边形BCPE是平行四边形，

∴PC∥BE，PC⊄平面EBD，BE⊂平面EBD，

∴PC∥平面EBD.

B组

5．(原创题)直线a∥平面α，α内有n条直线交于一点，则这n条直线中与直线a平行的直线有________条．

答案：1或0