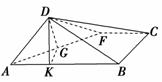
6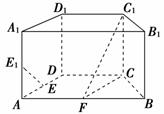．(2009年高考山东卷)如图，在直四棱柱ABCD－A₁B₁C₁D₁中，底面ABCD为等腰梯形，AB∥CD，AB＝4，BC＝CD＝2，AA₁＝2，E，E₁分别是棱AD，AA₁的中点．

(1)设F是棱AB的中点，证明：直线EE₁∥平面FCC₁；

(2)证明：平面D₁AC⊥平面BB₁C₁C.

证明：(1)法一：取A₁B₁的中点为F₁，连结FF₁，C₁F₁.

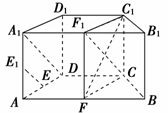由于FF₁∥BB₁∥CC₁，

所以F₁∈平面FCC₁.

因此平面FCC₁即为平面C₁CFF₁.

连结A₁D，F₁C，

由于A₁F₁綊D₁C₁綊CD，

所以四边形A₁DCF₁为平行四边形，

因此A₁D∥F₁C.又EE₁∥A₁D，

得EE₁∥F₁C.

而EE₁⊄平面FCC₁，F₁C⊂平面FCC₁，

故EE₁∥平面FCC₁.

法二：因为F为AB的中点，

CD＝2，AB＝4，AB∥CD，

所以CD綊AF，

因此四边形AFCD为平行四边形，

所以AD∥FC.

又CC₁∥DD₁，FC∩CC₁＝C，FC⊂平面FCC₁，CC₁⊂平面FCC₁，AD∩DD₁＝D，AD⊂平面ADD₁A₁，DD₁⊂平面ADD₁A₁.

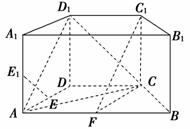所以平面ADD₁A₁∥平面FCC₁.

又EE₁⊂平面ADD₁A₁，所以EE₁∥平面FCC₁.

(2)连结AC，在△FBC中，FC＝BC＝FB，

又F为AB的中点，所以AF＝FC＝FB.

因此∠ACB＝90°，即AC⊥BC.

又AC⊥CC₁，且CC₁∩BC＝C，

所以AC⊥平面BB₁C₁C.

而AC⊂平面D₁AC，

故平面D₁AC⊥平面BB₁C₁C.

B组

5．(原创题)已知a、b为两条不同的直线，α、β为两个不同的平面，且a⊥α，b⊥β，则下列命题中假命题的有________．

①若a∥b，则α∥β；②若α⊥β，则a⊥b；③若a、b相交，则α、β相交；④若α、β相交，则a，b相交．

解析：若α、β相交，则a、b既可以是相交直线，也可以是异面直线．

答案：④

4．(2009年高考浙江卷)如图，在长方形ABCD中，AB＝2，BC＝1，E为DC的中点，F为线段EC(端点除外)上一动点．现将△AFD沿AF折起，使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB，K为垂足．设AK＝t，则t的取值范围是________．

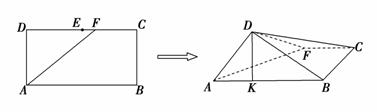
解析：如图，过D作DG⊥AF，垂足为G，连结GK，∵平面ABD⊥平面ABC，又DK⊥AB，

∴DK⊥平面ABC，∴DK⊥AF.

∴AF⊥平面DKG，∴AF⊥GK.

容易得到，当F接近E点时，K接近AB的中点，当F接近C点时，K接近AB的四等分点．∴t的取值范围是(，1)．答案：(，1)

3．(2009年高考山东卷改编)已知α、β表示两个不同的平面，m为平面α内的一条直线，则“α⊥β ”是“m⊥β ”的________条件．

解析：由平面与平面垂直的判定定理知如果m为平面α内的一条直线，m⊥β，则α⊥β，反过来则不一定．所以“α⊥β”是“m⊥β”的必要不充分条件．

答案：必要不充分

2．(2010年青岛质检)已知直线l⊥平面α，直线m⊂平面β，下面有三个命题：

①α∥β⇒l⊥m；②α⊥β⇒l∥m；③l∥m⇒α⊥β.则真命题的个数为________．

解析：对于①，由直线l⊥平面α，α∥β，得l⊥β，又直线m⊂平面β，故l⊥m，故①正确；对于②，由条件不一定得到l∥m，还有l与m垂直和异面的情况，故②错误；对于③，显然正确．故正确命题的个数为2.答案：2个

1．(2010年宁波十校联考)设b、c表示两条直线，α，β表示两个平面，则下列命题是真命题的是________．

①若b⊂α，c∥α，则b∥c　②若b⊂α，b∥c，则c∥α

③若c∥α，α⊥β，则c⊥β　 ④若c∥α，c⊥β，则α⊥β

解析：①中，b，c亦可能异面；②中，也可能是c⊂α；③中，c与β的关系还可能是斜交、平行或c⊂β；④中，由面面垂直的判定定理可知正确．

答案：④

12．如图，四边形ABCD为矩形，BC⊥平面ABE，F为CE上的点，且BF⊥平面ACE.

(1)求证：AE⊥BE；

(2)设点M为线段AB的中点，点N为线段CE的中点．求证：MN∥平面DAE.

证明：(1)因为BC⊥平面ABE，AE⊂平面ABE，

所以AE⊥BC，

又BF⊥平面ACE，AE⊂平面ACE，

所以AE⊥BF，

又BF∩BC＝B，所以AE⊥平面BCE，

又BE⊂平面BCE，所以AE⊥BE.

(2)取DE的中点P，连结PA，PN，因为点N为线段CE的中点．

所以PN∥DC，且PN＝DC，

又四边形ABCD是矩形，点M为线段AB的中点，所以AM∥DC，且AM＝DC，

所以PN∥AM，且PN＝AM，故四边形AMNP是平行四边形，所以MN∥AP，

而AP⊂平面DAE，MN⊄平面DAE，所以MN∥平面DAE.

第四节　　 垂直关系

A组

11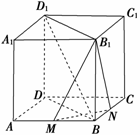．(2010年扬州调研)在正方体ABCD－A₁B₁C₁D₁中，M，N分别是AB，BC的中点．

(1)求证：平面B₁MN⊥平面BB₁D₁D；

(2)若在棱DD₁上有一点P，使BD₁∥平面PMN，求线段DP与PD₁的比

解：(1)证明：连结AC，则AC⊥BD ，

又M，N分别是AB，BC的中点，

∴MN∥AC，∴MN⊥BD.

∵ABCD－A₁B₁C₁D₁是正方体，

∴BB₁⊥平面ABCD，

∵MN⊂平面ABCD，

∴BB₁⊥MN，

∵BD∩BB₁＝B，

∴MN⊥平面BB₁D₁D，

∵MN⊂平面B₁MN，

∴平面B₁MN⊥平面BB₁D₁D.

(2)设MN与BD的交点是Q，连结PQ，PM，PN

∵BD₁∥平面PMN，BD₁⊂平面BB₁D₁D，平面BB₁D₁D∩平面PMN＝PQ，

∴BD₁∥PQ，

∴DP∶PD₁＝DQ∶QB＝3∶1.

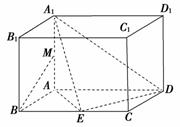
10．如图，长方体ABCD－A₁B₁C₁D₁中，AA₁＝，AB＝1，AD＝2，E为BC的中点，点M为棱AA₁的中点．

(1)证明：DE⊥平面A₁AE；

(2)证明：BM∥平面A₁ED.

证明：(1)在△AED中，AE＝DE＝，AD＝2，

∴AE⊥DE.

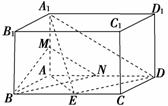∵A₁A⊥平面ABCD，

∴A₁A⊥DE，

∴DE⊥平面A₁AE.

(2) 设AD的中点为N，连结MN、BN.

在△A₁AD中，AM＝MA₁，AN＝ND，∴MN∥A₁D，

∵BE∥ND且BE＝ND，

∴四边形BEDN是平行四边形，

∴BN∥ED，

∴平面BMN∥平面A₁ED，

∴BM∥平面A₁ED.

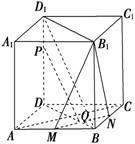
9．如图所示，在正方体ABCD－A₁B₁C₁D₁中，E、F、G、H分别是棱CC₁、C₁D₁、D₁D、CD的中点，N是BC中点．点M在四边形EFGH上及其内部运动，则M满足条件________时，有MN∥平面B₁BDD₁.

答案：M∈FH