12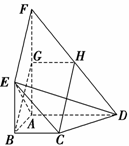．(2008年高考四川卷)如图，平面ABEF⊥平面ABCD，四边形ABEF与ABCD都是直角梯形，∠BAD＝∠FAB＝90°，BC綊AD，BE綊FA，G、H分别为FA、FD的中点．

(1)证明：四边形BCHG是平行四边形；

(2)C、D、F、E四点是否共面？为什么？

(3)设AB＝BE，证明：平面ADE⊥平面CDE.

解：(1)证明：由题设知，FG＝GA，FH＝HD，

所以GH綊AD.又BC綊AD，故GH綊BC.所以四边形BCHG是平行四边形．

(2)C、D、F、E四点共面．理由如下：

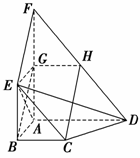由BE綊AF，G是FA的中点知，BE綊GF，所以EF∥BG.

由(1)知BG∥CH，所以EF∥CH，故EC、FH共面．

又点D在直线FH上，所以C、D、F、E四点共面．

(3)证明：连结EG.由AB＝BE，BE綊AG及∠BAG＝90°知ABEG是正方形，

故BG⊥EA.由题设知，FA、AD、AB两两垂直，故AD⊥平面FABE，

因此EA是ED在平面FABE内的射影．根据三垂线定理，BG⊥ED.

又ED∩EA＝E，所以BG⊥平面ADE.

由(1)知，CH∥BG，所以CH⊥平面ADE.

由(2)知F∈平面CDE，故CH⊂平面CDE，得平面ADE⊥平面CDE.

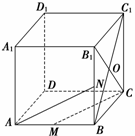
11．如图，在棱长为1的正方体ABCD－A₁B₁C₁D₁中，M为AB的中点，N为BB₁的中点，O为平面BCC₁B₁的中心．

(1)过O作一直线与AN交于P，与CM交于Q(只写作法，不必证明)；

(2)求PQ的长．

解：(1)连结ON，由ON∥AD知，AD与ON确定一个平面α.又O、C、M三点确定一个平面β(如图所示)．

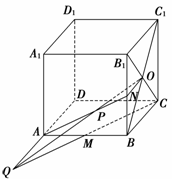∵三个平面α，β和ABCD两两相交，有三条交线OP、CM、DA，其中交线DA与交线CM不平行且共面．

∴DA与CM必相交，记交点为Q，∴OQ是α与β的交线．

连结OQ与AN交于P，与CM交于Q，

故直线OPQ即为所求作的直线．

(2)在Rt△APQ中，易知AQ＝1，又易知△APQ ∽△OPN，

∴＝＝2，AN＝，∴AP＝，

∴PQ＝＝.

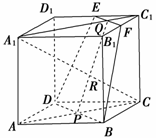
10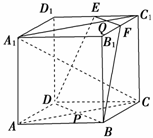．如图，已知正方体ABCD－A₁B₁C₁D₁中，E、F分别为D₁C₁、B₁C₁的中点，AC∩BD＝P，A₁C₁∩EF＝Q，若A₁C交平面DBFE于R点，试确定R点的位置．

解：在正方体AC₁中，连结PQ，

∵Q∈A₁C₁，∴Q∈平面A₁C₁CA.又Q∈EF，

∴Q∈平面BDEF，即Q是平面A₁C₁CA与平面BDEF的公共点，

同理，P也是平面A₁C₁CA与平面BDEF的公共点．

∴平面A₁C₁CA∩平面BDEF＝PQ.

又A₁C∩平面BDEF＝R，

∴R∈A₁C，

∴R∈平面A₁C₁CA，

R∈平面BDEF.

∴R是A₁C与PQ的交点．如图．

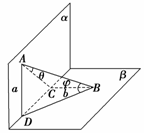
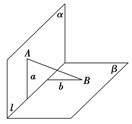
9.(2008年高考陕西卷改编)如图，α⊥β，α∩β=l，A∈α，B∈β，A、B到l的距离分别是a和b，AB与α、β所成的角分别是θ和φ，AB在α、β内的射影分别是m和n.若a＞b，则θ与φ的大小关系为______，m与n的大小关系为______.

解析：AB与β成的角为∠ABC＝φ，

AB与α成的角为∠BAD＝θ，

sin φ＝sin∠ABC＝，

sinθ＝sin∠BAD＝.

∵a>b，∴sinφ>sinθ.∴θ<φ.

AB在α内的射影AD＝，

AB在β内的射影BC＝，

∴AD.BC，即m>n.

答案：θ＜φ　m＞n

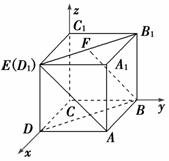
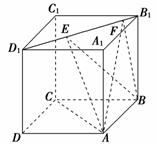
8．(2009年高考宁夏、海南卷改编)如图所示，正方体ABCD－A₁B₁C₁D₁的棱长为1，线段B₁D₁上有两个动点E，F，且EF＝，则下列结论中错误的是________．

①AC⊥BE

②EF∥平面ABCD

③三棱锥A－BEF的体积为定值

④异面直线AE，BF所成的角为定值

解析：∵AC⊥平面BB₁D₁D，又BE⊂平面BB₁D₁D，

∴AC⊥BE.故①正确．

∵B₁D₁∥平面ABCD，又E、F在直线D₁B₁上运动，

∴EF∥平面ABCD.故②正确．

③中由于点B到直线B₁D₁的距离不变，故△BEF的面积为定值．又点A到平面BEF的距离为，故V_A－BEF为定值．

当点E在D₁处，F为D₁B₁的中点时，

建立空间直角坐标系，如图所示，可得A(1,1,0)，B(0,1,0)，E(1,0,1)，F.∴A＝(0，－1,1)，B＝(，－，1)，

∴A·B＝.又||＝，||＝，∴cos〈A，B〉＝＝，

∴AE与BF成30°角．当E为D₁B₁中点，F在B₁处时，

此时E，F(0,1,1)，∴A＝，B＝(0,0,1)，

∴A·B＝1，|A|＝ ，∴cos〈A，B〉＝ ＝≠.故④错．

答案：④

7．(2009年高考广东卷改编)给定下列四个命题：

①若一个平面内的两条直线与另一个平面平行，那么这两个平面相互平行；

②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；

③垂直于同一直线的两条直线相互平行；

④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．

其中，为真命题的是________．

解析：当两个平面相交时，一个平面内的两条直线可以平行于另一个平面，故①不对；由平面与平面垂直的判定定理可知②正确；空间中垂直于同一条直线的两条直线可以平行，相交也可以异面，故③不对；若两个平面垂直，只有在一个平面内与它们的交线垂直的直线才与另一个平面垂直，故④正确．答案：②④

6．(2010年湖南郴州调研)设α，β，γ是三个不重合的平面，l是直线，给出下列四个命题：

①若α⊥β，l⊥β，则l∥α；

②若l⊥α，l∥β，则α⊥β；

③若l上有两点到α的距离相等，则l∥α；

④若α⊥β，α∥γ，则γ⊥β.

其中正确命题的序号是________．

解析：①错误，l可能在平面α内；②正确，l∥β，l⊂γ，β∩γ＝n⇒l∥n⇒n⊥α，则α⊥β；③错误，直线可能与平面相交；④正确．故填②④.答案：②④

5．正方体AC₁中，E、F分别是线段C₁D、BC的中点，则直线A₁B与直线EF的位置关系是________．

解析：直线AB与直线外一点E确定的平面为A₁BCD₁，EF⊂平面A₁BCD₁，且两直线不平行，故两直线相交．答案：相交

4．(2008年高考浙江卷改编)对两条不相交的空间直线a与b，必存在平面α，使得________．

①a⊂α，b⊂α　　②a⊂α，b∥α　　 ③a⊥α，b⊥α　④a⊂α，b⊥α

解析：不相交的直线a、b的位置有两种：平行或异面．当a、b异面时，不存在平面α满足①、③；又只有当a⊥b时④才成立．答案：②

3．对于空间三条直线，有下列四个条件：

①三条直线两两相交且不共点②三条直线两两平行③三条直线共点

④有两条直线平行，第三条直线和这两条直线都相交

其中使三条直线共面的充分条件有：________.

解析：易知①中的三条直线一定共面，④中两条直线平行可确定一个平面，第三条直线和这两条直线相交于两点，则第三条直线也在这个平面内，故三条直线共面．答案：①④