2．(2010年浙江杭州名校一模)直线y＝x+3与曲线－＝1交点的个数为(　)

A．0　 　　　　　　　　　　　　　　　　　　　　　　 B．1

C．2　 　　　　　　　　　　　　　　　　　　　　　　 D．3

[解析]　x＞0，曲线为－＝1；x＜0，曲线为+＝1，画图可知，直线与曲线的交点个数为3个．

[答案]　D

1．(2010年安徽模拟)已知曲线+＝1和直线ax+by+1＝0(a，b为非零实数)，在同一坐标系中，它们的图形可能是(　)

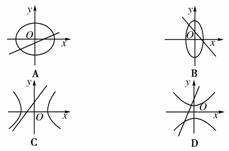
[答案]　C

12．已知O为坐标原点，A(2,1)，P(x，y)满足，求||·cos∠AOP的最大值．

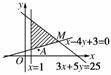[解析]　在平面直角坐标系中画出不等式组所表示的可行域(如图)，

由于||·cos∠AOP＝

＝

而＝(2,1)，＝(x，y)

所以||·cos∠AOP＝，

令z＝2x+y，则y＝－2x+z，即z表示直线y＝－2x+z在y轴上的截距，

由图形可知，当直线经过可行域中的点M时，z取到最大值．

由得M(5,2)，这时z＝12，

此时||·cos∠AOP＝＝，

故||·cos∠AOP的最大值等于.

11．(2010年黄冈模拟)某研究所计划利用“神七”宇宙飞船进行新产品搭载实验，计划搭载新产品A、B，该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排，通过调查，有关数据如表：

试问：如何安排这两种产品的件数进行搭载，才能使总预计收益达到最大，最大收益是多少？

[解析]　设搭载产品A有x件，产品B有y件，

预计收益z＝80x+60y.

则，作出可行域，如图

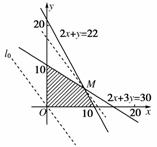
作出直线l₀：4x+3y＝0并平移，由图象得，当直线经过M点时z能取得最大值，，

解得即M(9,4)．

所以z_max＝80×9+60×4

＝960(万元)．

答：搭载产品A 9件，产品B 4件，可使得总预计收益最大，为960万元．

10．若a≥0，b≥0，且当时，恒有ax+by≤1，求以a，b为坐标的点P(a，b)所形成的平面区域的面积．

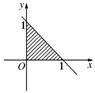
[解析]　作出线性约束条件

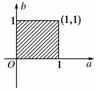，对应的可行域如图所示，

在此条件下，要使ax+by≤1恒成立，只要ax+by的最大值不超过1即可．

令z＝ax+by，则y＝－x+.

因为a≥0，b≥0，

则－1＜－≤0时，

b≤1或－≤－1时，a≤1，

此时对应的可行域如图，

所以以a，b为坐标的点P(a，b)所形成的平面区域的面积为1.

9．设D是不等式组表示的平面区域，则D中的点P(x，y)到直线x+y＝10距离的最大值是______．

[解析]　画出可行域，由图知最优解为A(1,1)，

故A到x+y＝10的距离为＝4.

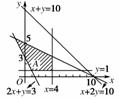
[答案]　4

8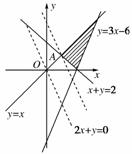．(2010年柳州模拟)已知x，y满足条件，则z＝2x+y的最小值为______．

[解析]　作出可行域．

由图可得目标函数过A点时，z最小．

由，得.

∴A(1,1)，∴z＝2x+y＝2×1+1＝3.

[答案]　3

7．由直线x+y+2＝0，x+2y+1＝0和2x+y+1＝0围成的三角形区域(含边界)用不等式组可表示为______．

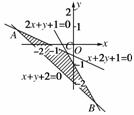[解析]　由直线围成的三角形区域如图阴影部分，

经判断知x+y+2≥0

2x+y+1≤0，x+2y+1≤0

[答案]　

6．下面给出的四个点中，到直线x－y+1＝0的距离为，且位于表示的平面区域内的点是(　)

A．(1,1)　　　　　　　　　　　　　　　　 B．(－1,1)

C．(－1，－1)　 　　　　　　　　　　　　　　　　　　 D．(1，－1)

[解析]　方法一：把(1,1)代入x+y－1得1+1－1＝1＞0，排除A；

把(－1,1)代入x－y+1得－1－1+1＝－1＜0，排除B；而(1，－1)到直线x－y+1＝0的距离为，排除D；故选C.

方法二：到直线x－y+1＝0的距离为的点的轨迹为两条直线x－y＝0，x－y+2＝0.

又由图形知选C.

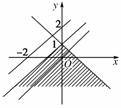
[答案]　C

5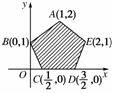．已知以x，y为自变量的目标函数ω＝kx+y(k＞0)的可行域如图阴影部分(含边界)所示，若使ω取最大值时的最优解有无穷多个，则k的值为(　)

A．1　 　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C．2　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．4

[解析]　由目标函数得y＝－kx+ω，可见直线y＝－kx+ω截距最大时ω值最大．由图象可知，直线y＝－kx+ω与AE所在的直线重合时截距最大且有无穷多个，

∵k_AE＝＝－1，∴－k＝k_AE＝－1，∴k＝1.

[答案]　A