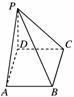
3．如图所示，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD，PD＝AD＝1，设点C到平面PAB的距离为d₁，点B到平面PAC的距离为d₂，则有(　)

A．1<d₁<d₂　 　　　　　　　　　　　　　　　　　　　　　　　　 B．d₁<d₂<1

C．d₁<1<d₂　 　　　　　　　　　　　　　　　　　　　　　　　　 D．d₂<d₁<1

[解析]　点C到平面PAB的距离d₁＝，点B到平面PAC的距离d₂＝，

∵<<1，∴d₂<d₁<1.

[答案]　D

2．若正棱锥的底面边长与侧棱长相等，则该棱锥一定不是(　)

A．三棱锥　 　　　　　　　　　　　　　　　　　　　　　　　　 B．四棱锥

C．五棱锥　 　　　　　　　　　　　　　　　　　　　　　　　　 D．六棱锥

[解析]　各侧面为正三角形，若为六棱锥则不能构成空间图形．

[答案]　D

1．若一个四棱柱的四个侧面都是正方形，则这个四棱柱是(　)

A．正方体　 　　　　　　　　　　　　　　　　　　　　　　　　 B．正四棱柱

C．长方体　 　　　　　　　　　　　　　　　　　　　　　　　　 D．直平行六面体

[答案]　D

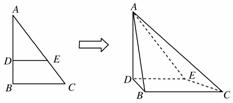
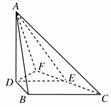
12．(2008年重庆高考题)如图所示，在△ABC中，∠B＝90°，AC＝，D、E两点分别在AB、AC上，使＝＝2，DE＝3.现将△ABC沿DE折成直二面角，求：

(1)异面直线 AD与BC的距离；

(2)二面角A-EC-B的大小(用反三角函数表示)．

[解析]　(1)因＝，故DE∥BC，又因∠B＝90°，从而AD⊥DE.

因A-DE-B是直二面角，AD⊥DE，故AD⊥底面DBCE，从而AD⊥DB.而DB⊥BC，故DB为异面直线AD与BC的公垂线．

由＝＝2，得＝＝.

又已知DE＝3，从而

BC＝DE＝.AB＝＝＝6.

因＝，故DB＝2，为所求异面直线AD与BC的距离．

(2)过D作DF⊥CE，交CE的延长线于F，连接AF.由(1)知，AD⊥底面DBCE，由三垂线定理知AF⊥FC，

故∠AFD为二面角A-EC-B的平面角．在底面DBCE中，∠DEF＝∠BCE，DB＝2，EC＝·＝，

因此sin∠BCE＝＝.

从而在Rt△DFE中，DE＝3，

DF＝DEsin∠DEF＝DEsin∠BCE＝3·＝.

在Rt△AFD中，AD＝4，tan∠AFD＝＝.

因此所求二面角A-EC-B的大小为arctan .

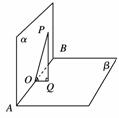
11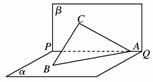．如图所示，已知直二面角α-PQ-β，A∈PQ，B∈α，C∈β，CA＝CB，∠BAP＝45°，直线CA和平面α所成的角为30°.

(1)证明BC⊥PQ；

(2)求二面角B-AC-P的大小．

[解析]　(1)证明：在平面β内过点C作CO⊥PQ于点O，连结OB.

因为α⊥β，α∩β＝PQ，所以CO⊥α.又因为CA＝CB，所以OA＝OB.而∠BAO＝45°，∴∠ABO＝45°，∠AOB＝90°，从而BO⊥PQ.又CO⊥PQ，

所以PQ⊥平面OBC.

因为BC⊂平面OBC，故PQ⊥BC.

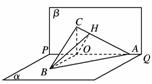
(2)由(1)知，BO⊥PQ，又α⊥β，α∩β＝PQ，

BO⊂α，所以BO⊥β.过点O作OH⊥AC于点H，连结BH，由三垂线定理知，BH⊥AC.

故∠BHO是二面角B-AC-P的平面角．

由(1)知，CO⊥α，所以∠CAO是CA和平面α所成的角，则∠CAO＝30°.不妨设AC＝2，则AO＝，OH＝AOsin 30°＝.在Rt△OAB中，∠ABO＝∠BAO＝45°，所以BO＝AO＝.

于是在Rt△BOH中，tan ∠BHO＝＝＝2.

故二面角B-AC-P的大小为arctan 2.

10．如图所示，四面体ABCS中，SA，SB，SC两两垂直，∠SBA＝45°，∠SBC＝60°，M为AB的中点．求：

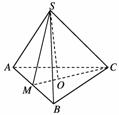(1)BC与平面SAB所成的角；

(2)SC与平面ABC所成角的正切值．

[解析]　(1)∵CS⊥SB，CS⊥SA，

∴SC⊥平面SAB，

∴BC在平面SAB上的射影为SB.

∴∠SBC为BC与平面SAB所成的角．

又∠SBC＝60°，

故BC与平面SAB所成的角为60°.

(2)连结MC，在Rt△ASB中，∠SBA＝45°，

∴SM⊥AB.

又AB⊥SC，∴AB⊥面SMC.

∴面SMC⊥面ABC.

过点S作SO⊥MC于点O，

∴SO⊥面ABC，

∴∠SCM为SC与平面ABC所成的角．

设SB＝a，则SM＝a，

在△SBC中，SC＝SBtan 60°＝a，

∴tan∠SCM＝＝.

9．已知点O在二面角α-AB-β的棱上，点P在α内，且∠POB＝45°.若对于β内异于O的任意一点Q，都有∠POQ≥45°，则二面角α-AB-β的大小是________．

[解析]　∵对于β内异于O的点Q，都有∠POQ≥45°，

∴PO与面β所成的角即为45°，若作PQ⊥β于Q点，则∠POQ＝45°，

∴Q∈AB.

又PQ⊂α，∴α⊥β即α-AB-β的大小为90°.

[答案]　90°

8．若一条直线与一个正四棱柱各个面所成的角都为α，则cos α＝________.

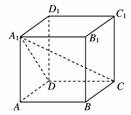[解析]　∵为填空题，∴不妨设正四棱柱为一个正方体．而在正方体中与各个面所成角相等的为体对角线，如图所示．

即图中∠CA₁D.而若令正方体棱长为1，则A₁D＝，

A₁C＝＝，

∴cos∠CA₁D＝＝.

[答案]　

7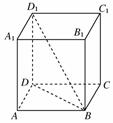．(2008年四川高考)已知正四棱柱的对角线的长为，且对角线与底面所成角的余弦值为，则该四棱柱的体积等于________．

[解析]　如图，设正四棱柱的底边长为a，高为h，

则对角线BD₁与底面所成的角为∠DBD₁，

由题意得

解得a＝1，h＝2，∴VABCD-A₁B₁C₁D₁＝a²h＝2.

[答案]　2

6．如图所示，过正方形ABCD的顶点A，引PA⊥平面ABCD，若PA＝AB，则平面ABP和平面CDP所成的二面角的大小是(　)

A．30°　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．45°

C．60°　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．90°

[解析]　过P作PQ∥AB.则PQ为面ABP与面CDP的交线，

∵AP⊥AB，∴AP⊥PQ.

又CD⊥AD且CD⊥AP，∴CD⊥DP，

即DP⊥PQ，所以∠DPA为所求的二面角的平面角．

显然∠DPA＝45°，故选B.

[答案]　B