11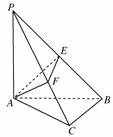．在空间四边形PABC中，PA⊥平面ABC，AC⊥BC.若A在PB、PC上的射影分别是E、F.求证：EF⊥PB.

[证明]　由已知可得

·＝0，·＝0，

·＝0，·＝0，

又、、共面，

所以存在实数x，y，使得＝x+y，

·＝(－)·

＝·＝·(+)

＝·＝(x+y)·

＝x(·)+y(·)

＝0+0＝0.

∴EF⊥PB.

10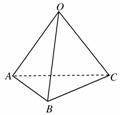．如图所示，在空间四边形OABC中，OA＝8，AB＝6，AC＝4，BC＝5，∠OAC＝45°，∠OAB＝60°，求OA与BC所成角的余弦值．

[解析]　∵B＝A－A，

O·B＝O·(A－A)

＝O·A－O·A

＝|O||A|cos〈O，A〉－|O||A|cos〈O，A〉

＝8×4×cos135°－8×6×cos120°＝24－16，

∴cos〈O，B〉＝＝＝，

故OA与BC所成角的余弦值为.

9．在各棱长都等于1的正四面体OABC中，若点P满足＝x·+y·+z·(其中x+y+z＝1)，则||的最小值等于________．

[解析]　由于＝x·+y·+z·，

所以||²＝(x·+y·+z·)²

＝x²+y²+z²+xy+yz+xz＝1－(xy－yz－xz)，

而1＝(x+y+z)²＝x²+y²+z²+2(xy+yz+xz)

≥3(xy+yz+xz)，所以xy+yz+xz≤，

于是||²≥，故||≥，

即||的最小值等于.

[答案]　

8．已知a＝(2,3，－1)，b＝(－2,1,3)，则以a，b为邻边的平行四边形的面积是________．

[解析]　∵a·b＝－4+3－3＝－4，

|a|＝|b|＝＝，

∴cos〈a，b〉＝－＝－，

∴sin〈a，b〉＝，

∴S_{平行四边形}＝|a||b|sin〈a，b〉＝14×＝6.

[答案]　6

7．已知平行六面体ABCD-A₁B₁C₁D₁，以顶点A为端点的三条棱长都是1，且两两夹角为60°，则对角线AC₁的长是________．

[解析]　∵＝++，

∴||²＝

＝(++)²

＝+++2·+2·+2·

＝1+1+1+2cos 60°×3＝6，

∴||＝.

[答案]　

6．将正△ABC沿其所在平面的法向量平移到△A₁B₁C₁，连接对应顶点，若AB＝BB₁，则AB₁与C₁B所成的角的大小为(　)

A．60°　 　　　　　　　　　　　　　　　　　　　　　　　　 B．90°

C．105°　 　　　　　　　　　　　　　　　　　　　　　　　 D．75°

[解析]　设与的夹角为θ，则

＝+，＝+.

不妨取BB₁＝1，AB＝，得AB₁＝，C₁B＝.

则·＝||||cos θ＝3cos θ.

又·＝(+)·(+)

＝·+·+·+·

＝0－1+×cos 60°+0＝0，

∴cos θ＝0，得θ＝90°，故选B.

[答案]　B

5．已知四边形ABCD满足：·>0，·>0，·>0，·>0，则该四边形为(　)

A．平行四边形　 　　　　　　　　　　　　　　　　　 B．梯形

C．平面四边形　 　　　　　　　　　　　　　　　　　 D．空间四边形

[解析]　由已知条件得四边形的四个外角均为锐角，但在平面四边形中任一四边形的外角和是360°，这与已知条件矛盾，所以该四边形是一个空间四边形．故选D.

[答案]　D

4．已知空间四边形ABCD的每条边和对角线的长都等于a，点E、F分别是BC、AD的中点，则·的值为(　)

A．a²　 　　　　　　　　　　　　　　　　　　　　　　　　　 B.a²

C.a²　 　　　　　　　　　　　　　　　　　　　　　　　　　 D.a²

[解析]　·＝(+)·

＝(·+·)

＝(a²cos 60°+a²cos 60°)＝a².

[答案]　C

3．在以下命题中，不正确的命题个数为(　)

①已知A、B、C、D是空间任意四点，则+++＝0.②|a|－|b|＝|a+b|是a，b共线的充分条件．③若a与b共线，则a与b所在直线平行．④对空间任意一点O和不共线的三点A、B、C，若＝x +y+z(其中x、y、z∈R)，则P、A、B、C四点共面．

A．1个　 　　　　　　　　　　　　　　　　　　　　　　　 B．2个

C．3个　 　　　　　　　　　　　　　　　　　　　　　　　 D．4个

[解析]　+++＝++＝+＝0，①正确；|a|－|b|＝|a|+|b|成立的充分条件是|a|与|b|共线且方向相反，且|a|>|b|，因此②错，由向量平行知③不正确，由空间向量中点共面知④不正确，故选C.

[答案]　C

2．已知向量a，b，c两两夹角都是60°，其模都是1，则|a－b+2c|等于(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．5

C．6　 　　　　　　　　　　　　　　　　　　　　　　　　　 D.

[解析]　∵(a－b+2c)²

＝a²+b²+4c²－2a·b－4b·c+4a·c

＝1+1+4－2×1×1×cos60°－4×1×1×cos60°+4×1×1×cos60°

＝6－1－2+2＝5，

∴|a－b+2c|＝.

[答案]　A