9．(2008年全国Ⅰ)已知菱形ABCD中，AB＝2，∠A＝120°，沿对角线BD将△ABD折起，使二面角A-BD-C为120°，则点A到△BCD所在平面的距离等于________．

[解析]　如图所示，取BD中点E，连接AE、CE.

∵△ABD、△BCD均为等腰三角形，∴AE⊥BD，CE⊥BD，

∴BD⊥平面AEC.

∴∠AEC为二面角A-BD-C的平面角，

∴∠AEC＝120°.

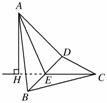在平面AEC内过A作CE的垂线AH，垂足为H，则H在CE的延长线上．

∵BD⊥平面AEC.

∴BD⊥AH.又AH⊥CE，

∴AH⊥平面BCD.

∵∠BAD＝120°，∴∠BAE＝60°，

∴cos∠BAE＝，∴AE＝1.

又∠AEH＝60°，∴AH＝.

[答案]　

8．如图所示，在△ABC中，∠ACB＝90°，AB＝8，∠BAC＝60°，PC⊥平面ABC，PC＝4，M为AC边上的一个动点，则PM的最小值为________．

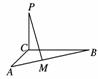[解析]　作CH⊥AB交AB于H，连结PH.∵PC⊥平面ABC，∴PH⊥AB，则当点M在H处时，PH最小．

∵AC＝8cos 60°＝4，∴CH＝4sin 60°＝2，

∴PH＝＝2，

即PM的最小值2.

[答案]　2

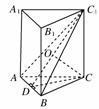
7．如图所示，在正三棱柱ABC-A₁B₁C₁中，AB＝1.若二面角C-AB-C₁的大小为60°，则点C到平面ABC₁的距离为________．

[解析]　如图所示，在△ABC中，AB＝1，则AB边上的高CD长度为，∠C₁DC＝60°.

∴CC₁＝，C₁D＝.

在△CDC₁中，CO⊥C₁D，

由图可知CO为面ABC₁的垂线，

∴由等面积法可得

C₁D·CO＝CD·CC₁.

∴CO＝.

[答案]　

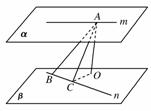
6．已知平面α∥平面β，直线m⊂α，直线n⊂β，点A∈m，点B∈n，记点A、B之间的距离为a，点A到直线n的距离为b，直线m和n的距离为c，则(　)

A．b≤c≤a　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．a≤c≤b

C．c≤a≤b　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．c≤b≤a

[解析]　如图：α∥β，考虑m，n异面时，m和n的距离等于α、β间距离，点A到n的距离可以如下作出：过A作AO⊥面β于O，过O作OC⊥n于C，则AC为A点到直线n的距离，显然，此时c≤b≤a，故选D.

[答案]　D

5．如图所示，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为和.过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB∶A′B′等于(　)

A．2∶1　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B．3∶1

C．3∶2　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D．4∶3

[解析]　由已知条件可知∠BAB′＝，∠ABA′＝，

设AB＝2a，经计算BB′＝a，A′B＝a，

∴在Rt△BB′A′中得A′B′＝a，

∴AB∶A′B′＝2∶1.

[答案]　A

4．空间四点A、B、C、D每两点的连线长都等于a，动点P在线段AB上，动点Q在线段CD上，则点P与Q的最小距离为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.a

C.a　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.a

[解析]　当P、Q为中点时，PQ为AB和CD的公垂线，此时最短，求出得PQ＝a.

[答案]　B

3．在棱长为1的正方体ABCD-A₁B₁C₁D₁中，E、F分别为棱AA₁、BB₁的中点，G为棱A₁B₁上的一点，且A₁G＝λ(0≤λ≤1)，则点G到平面D₁EF的距离为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

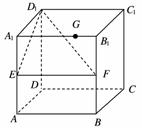[解析]　A₁B₁∥面D₁EF，∴G到面D₁EF的距离为A₁到面D₁EF的距离．在△A₁D₁E中，过A₁作A₁H⊥D₁E交D₁E于H，显然A₁H⊥面D₁EF，则A₁H即为所求，在Rt△A₁D₁E中，A₁H＝＝＝.

[答案]　D

2．在正三棱锥P-ABC中，三条侧棱两两互相垂直，侧棱长为a，则点P到平面ABC的距离为(　)

A．a　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.a

C.a　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.a

[解析]　作PH⊥平面ABC于H，连结CH并延长，交AB于D，连结PD，由PH·CD＝PC·PD，求得PH＝a.

[答案]　C

1．平面α内的∠MON＝60°，PO是α的斜线，PO＝3，∠POM＝∠PON＝45°，那么点P到平面α的距离是(　)

A.　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

[解析]　cos ∠POM＝cos ∠POH·cos ∠MOH，

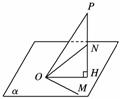∴＝cos ∠POH.

∴cos ∠POH＝.

∴sin ∠POH＝，

∴PH＝PO·sin ∠POH＝3×＝.

[答案]　A

12．在平行四边形ABCD中，AB＝AC＝1，∠ACD＝90°，将它沿对角线AC折起，使AB与CD成60°角，求B、D之间的距离．

[解析]　如图(1)、(2)

∵∠ACD＝90°，∠BAC＝90°，

∴·＝0，·＝0.

∵AB与CD所成的角为60°.

∴〈，〉＝60°或120°.

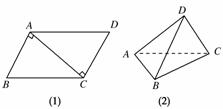
又＝++，

∴＝(++)²

＝+++2·+2·+2·

＝1+1+1+0－2··+0

＝3－2·cos〈，〉．

若〈，〉＝60°，则＝2，||＝.

若〈，〉＝120°，则＝4，||＝2.

因此，B、D之间的距离为或2.