
题目列表(包括答案和解析)
7. 若不等式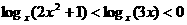 成立,则实数x的取值范围是____________.
成立,则实数x的取值范围是____________.
6. 若不等式 对
对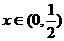 恒成立,则实数a的取值范围是 ( )
恒成立,则实数a的取值范围是 ( )
A. 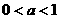 B.
B. 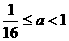 C.
C.  D.
D. 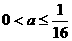
5.定义在R上的偶函数f(x)满足f(x)=f(x+2),当x∈[3, 4]时,f(x)=x-2,则 ( )
A.f(sin )<f(cos
)<f(cos )
B.f(sin
)
B.f(sin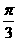 )>f(cos
)>f(cos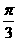 )
)
C.f(sin1)<f(cos1) D.f(sin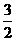 )>f(cos
)>f(cos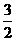 )
)
4. 已知函数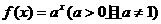 在区间[-2,2]上的植域不大于2,则函数
在区间[-2,2]上的植域不大于2,则函数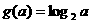 的值域是 ( )
的值域是 ( )
A.  B.
B. 
C.  D.
D. 
3. 函数 的值域是 ( )
的值域是 ( )
A. 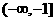 B.
B.  C.
C.  D.
D.
2.设函数f(x)=logax(a>0,a≠1),满足f(9)=2,则f-1(log92)的值是 ( )
A.log3 B.
B.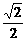 C.
C. D.2
D.2
1.设函数f(x)= ,若f(x0)>1,则x0的取值范围是 ( )
,若f(x0)>1,则x0的取值范围是 ( )
A.(-1, 1) B.(-1, +∞)
C.(-∞, -2)∪(0, +∞) D.(-∞, -1)∪(1, +∞)
18. 解:(1)由题意知{xn}为等比数列,且xn>0,又yn=2logaxn,则yn+1-yn=2logaxn+1-2logaxn=2loga ,
,
∵{xn}为等比数列,则 为常数,∴yn+1-yn为常数,∴{yn}为等差数列,设公差为d.则y6-y3=3d=12-18=-6. ∴d=-2.∴yn=y3+(n-3)×d=18+(n-3)×(-2)=24-2n, ∴y1=22,
为常数,∴yn+1-yn为常数,∴{yn}为等差数列,设公差为d.则y6-y3=3d=12-18=-6. ∴d=-2.∴yn=y3+(n-3)×d=18+(n-3)×(-2)=24-2n, ∴y1=22,
Sn= ,显然n=11或n=12时,Sn取得最大值,且最大值为132.
,显然n=11或n=12时,Sn取得最大值,且最大值为132.
(2)∵yn=24-2n=2logaxn, ∴xn=a12-n,又xn>1,即a12-n>1.当a>1时,12-n>0,即n<12.当0<a<1时,12-n<0,即n>12.∴当0<a<1时,存在M=12时,当n>M时xn>1恒成立.
(3)an=log xn+1=
xn+1= , ∵an在(13, +∞)上为减函数,∴an>an+1.
, ∵an在(13, +∞)上为减函数,∴an>an+1.
17. 解: (1) 
 ,由此可得
,由此可得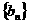 是等比数列
是等比数列
且首项 。
。
(2) ,∴
,∴ 是首项
是首项 的等差数列,
的等差数列,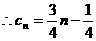 。
。
16. 解:(1)∵f(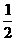 )+f(1-
)+f(1-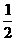 )=f(
)=f(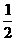 )+f(
)+f(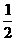 )=
)=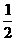 . ∴f(
. ∴f(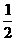 )=
)= .令x=
.令x=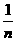 ,得f(
,得f(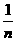 )+f(1-
)+f(1-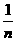 )=
)=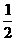 ,
,
即f(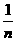 )+f(
)+f( )=
)=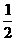 .
.
(2)an=
f(0)+f(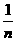 )+…+f(
)+…+f( )+f(1), an=f(1)+f(
)+f(1), an=f(1)+f( )+…+f(
)+…+f(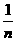 )+f(0),以上两式相加,得2an=[f(0)+f(1)]+[f(
)+f(0),以上两式相加,得2an=[f(0)+f(1)]+[f(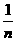 )+f(
)+f( )]+…+[f(1)+f(0)]=
)]+…+[f(1)+f(0)]= .∴an=
.∴an= , n∈N. an+1-an=
, n∈N. an+1-an= ,
,
故数列{an}是等差数列.
(3)bn= ,Tn=
,Tn=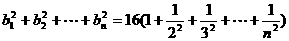
≤16[1+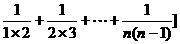 =16[1+(1-
=16[1+(1-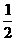 )+(
)+( )+…+(
)+…+(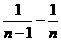 )]=16(2-
)]=16(2-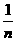 )=32-
)=32- =Sn.
=Sn.
∴Tn≤Sn.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com