8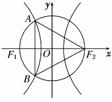．如右图，F₁和F₂分别是双曲线－＝1(a>0，b>0)的

两个焦点，A和B是以O为圆心，以|OF₁|为半径的圆

与该双曲线左支的两个交点，且△F₂AB是等边三角形，

则双曲线的离心率为　　　　　 　　 　　　　　　　　　　　　　　 (　)

A. 　　　　　B.　　　　 C.　 　　　　　　　D．1+

解析：连结AF₁，则∠F₁AF₂＝90°，∠AF₂B＝60°，

∴|AF₁|＝|F₁F₂|＝c，

|AF₂|＝|F₁F₂|＝c，

∴c－c＝2a，∴e＝＝＝1+.

答案：D

7．过点(0,1)的直线与x²+y²＝4相交于A、B两点，则|AB|的最小值为　　　　　　 (　)

A．2　 　　　　　　B．2 　　　　　C．3 　　　　　　　D．2

解析：当过点(0,1)的直线与直径垂直且(0,1)为垂足时，|AB|最小值为2.

答案：B

6．(2010·广州调研)已知点A(1,0)，直线l：y＝2x－4，点R是直线l上的一点，若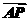＝，则点P的轨迹方程为　 　　　　　　　　　　　　　　　　　　　(　)

A．y＝－2x　　　　　 　B．y＝2x　　　　 C．y＝2x－8 　　　　D．y＝2x+4

解析：设点P(x，y)，R(x₁，y₁)，∵＝，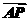

∴(1－x₁，－y₁)＝(x－1，y)，

∴即

又点R在直线l上，∴－y＝2(2－x)－4，

即2x－y＝0为所求．

答案：B

5．直线2x－y－2＝0绕它与y轴的交点逆时针旋转所得的直线方程是　　　　 (　)

A．－x+2y－4＝0 　　　　　　　　B．x+2y－4＝0

C．－x+2y+4＝0 　　　　　　　　D．x+2y+4＝0

解析：由题意知，两直线垂直，且已知直线过点(0，－2)，所求直线斜率为－，∴所求直线方程为y+2＝－x，即x+2y+4＝0.

答案：D

4．(2010·厦门质检)直角坐标平面内过点P(2,1)且与圆x²+y²＝4相切的直线　 (　)

A．有两条　 　　　　　　　B．有且仅有一条

C．不存在　 　　　　　　　D．不能确定

解析：∵2²+1²>4，∴点P在圆外，故过点P与圆相切的直线有两条．

答案：A

3．若双曲线－y²＝1的一个焦点为(2,0)，则它的离心率为　　　　　　　　 (　)

A. 　　　　　　B.　　　　　　 C. 　　　　　　　D．2

解析：由题意知a²+1＝4，∴a＝，∴e＝＝＝.

答案：C

2．(2010·苏州模拟)若ab<0，则过点P与Q的直线PQ的倾斜角的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　 　　　　　　　　B.　　　　　　 C.　 　　　D.

解析：k_PQ＝＝，∵ab<0，∴<0，即k<0，

∴直线PQ的倾斜角的取值范围是.

答案：B

1．(2009·天津河西期末)点P(－2,1)到直线2x+y＝5的距离为　　　　　　　　 (　)

A.　　　　　B.　　　　　　　　 C.　 　　　　　　　　D.

解析：点P到直线的距离d＝＝.

答案：B

22.(文)(本小题满分14分)已知m∈R，对p：x₁和x₂是方程x²－ax－2＝0的两个根，不等　 式|m－5|≤|x₁－x₂|对任意实数a∈恒成立；q：函数f(x)＝3x²+2mx+m+有两个不同的零点.求使“p且q”为真命题的实数m的取值范围.

解：由题设知x₁+x₂＝a，x₁x₂＝－2，

∴|x₁－x₂|＝＝.

a∈时，的最小值为3，要使|m－5|≤|x₁－x₂|对任意实数a∈恒成立，只需|m－5|≤3，即2≤m≤8.

由已知，得f(x)＝3x²+2mx+m+＝0的判别式

Δ＝4m²－12(m+)＝4m²－12m－16＞0，

得m＜－1或m＞4.

，综上，要使“p且q”为真命题，只需p真q真，

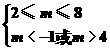
即　　　　　　　　 解得实数m的取值范围是(4,8].

(理)(本小题满分14分)设命题p：函数f(x)＝lg(ax²－x+a)的定义域为R；命题q：不等式＜1+ax对一切正实数均成立，如果命题p或q为真命题，命题p且q为假命题，求实数a的取值范围.

解：命题p为真命题⇔函数f(x)＝lg(ax²－x+a)的定义域为R，

即ax²－x+a＞0对任意实数x均成立，

得a＝0时，－x＞0的解集为R，不可能；

或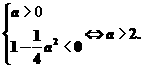　　　　　　　

a＜0时，ax²－x+解集显然不为R，

所以命题p为真命题⇔a＞2.

命题q为真命题⇔－1＜ax对一切正实数均成立，即a＞＝对一切正实数x均成立.

由于x＞0，所以＞1.

所以+1＞2，所以＜1.

所以，命题q为真命题⇔a≥1.

∵p或q为真命题，p且q为假命题，

∴p、q一真一假.

若p为真命题，q为假命题，无解；

若p为假命题，q为真命题，则1≤a≤2.

∴a的取值范围是.

21.(本小题满分12分)设全集是实数集R，A＝{x|2x²－7x+3≤0}，

B＝{x|x²+a<0}.

(1)当a＝－4时，求A∩B和A∪B；

(2)若(∁_RA)∩B＝B，求实数a的取值范围.

解：(1)∵A＝{x|≤x≤3}，

当a＝－4时，B＝{x|－2<x<2}，

∴A∩B＝{x|≤x<2}，A∪B＝{x|－2<x≤3}.

(2)∁_RA＝{x|x<或x>3}，

当(∁_RA)∩B＝B时，B⊆∁_RA，

①当B＝∅，即a≥0时，满足B⊆∁_RA；

②当B≠∅，即a<0时，B＝{x|－<x<}，要使B⊆∁_RA，需≤，解得－ ≤a<0.

综上可得，实数a的取值范围是a≥－.