
题目列表(包括答案和解析)
6.(2009·山东高考)集合A={0,2,a},B={1,a2}.若A∪B={0,1,2,4,16},则a的值为( )
A.0 B.1 C.2 D.4
解析:∵A∪B={0,1,2,a,a2},又A∪B={0,1,2,4,16},
∴{a,a2}={4,16},∴a=4.
答案:D
5.(2009·江苏高考)已知集合A={x|log2x≤2},B=(-∞,a),若A⊆B,则实数a的取值范围是(c,+∞),其中c= .
解析:A={x|0<x≤4},B=(-∞,a).
若A⊆B,则a>4.
即a的取值范围为(4,+∞),∴c=4.
答案:4
|
题组三 |
集合的基本运算 |
4.已知集合A={x|x2+x-6=0},B={x|mx+1=0},若B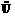 A,则实数m的取值集合是( )
A,则实数m的取值集合是( )
A.{-,0,} B.{0,1} C.{-,} D.{0}
解析:由x2+x-6=0得x=2或x=-3,
∴A={2,-3}.
又∵B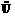 A,
A,
∴当m=0时,B=∅,满足条件;
当m≠0时,B={-},∴-=2或-=-3,
即m=-或m=.
答案:A
3.已知全集U=R,则正确表示集合M={-1,0,1}和N={x|x2+x=0}关系的韦恩(Venn)图是 ( )

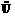 解析:∵M={-1,0,1},N={0,-1},∴N
M.
解析:∵M={-1,0,1},N={0,-1},∴N
M.
答案:B
2.已知集合A={a,b,2},B={2,b2,2a},则A∩B=A∪B,则a= .
解析:由A∩B=A∪B知A=B,又根据集合元素的互异性,所以有
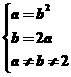
 或
或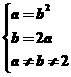 ,解得
,解得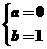 或
或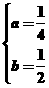

故a=0或
答案:0或
|
题组二 |
集合间的基本关系 |
1.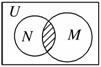 (2009·广东高考)已知全集U=R,集合M={x|-2≤x-1≤2}和
(2009·广东高考)已知全集U=R,集合M={x|-2≤x-1≤2}和
N={x|x=2k-1,k=1,2,…}的关系的韦恩(Venn)图如图所
示,则阴影部分所示的集合的元素共有 ( )
A.2个 B.3个 C.1个 D.无穷多个
解析:M={x|-1≤x≤3},N={x|x=2k-1,k∈N*},
∴M∩N={1,3}.
答案:A
22.(本小题满分14分)抛物线的顶点在原点,焦点在x轴的正半轴上,直线x+y-1=0与抛物线相交于A、B两点,且|AB|=.
(1)求抛物线的方程;
(2)在x轴上是否存在一点C,使△ABC为正三角形?若存在,求出C点的坐标;若不存在,请说明理由.
解:(1)设所求抛物线的方程为y2=2px(p>0),
由消去y,得x2-2(1+p)x+1=0,
设A(x1,y1),B(x2,y2),
则x1+x2=2(1+p),x1·x2=1.
∵|AB|=,
∴=,
∴121p2+242p-48=0.
∴p=或-(舍).
∴抛物线的方程为y2=x.
(2)设AB的中点为D,则D(,-).
假设x轴上存在满足条件的点C(x0,0),
∵△ABC为正三角形,∴CD⊥AB,∴kCD=1,
∴x0=.
∴C(,0),∴|CD|=.
又∵|CD|=|AB|=,故矛盾,
∴x轴上不存在点C,使△ABC为正三角形.
21.(本小题满分12分)椭圆+=1(a>b>0)的一个顶点为A(0,2),离心率e=.
(1)求椭圆的方程;
(2)直线l:y=kx-2(k≠0)与椭圆相交于不同的两点M、N,且满足 =
=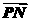 ,
,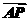 ·
· =0,求直线l的方程.
=0,求直线l的方程.
解:(1)设c=,依题意
得
即
∴a2=3b2=12,即椭圆方程为+=1.
(2)∵ =
=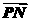 ,
,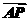 ·
·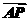 =0,∴AP⊥MN,
=0,∴AP⊥MN,
且点P是线段MN的中点,由
消去y得x2+3(kx-2)2=12,
即(1+3k2)x2-12kx=0,(*)
由k≠0,得方程(*)中Δ=(-12k)2=144k2>0,显然方程(*)有两个不相等的实数根.
设M(x1,y1)、N(x2,y2),线段MN的中点P(x0,y0),
则x1+x2=,∴x0==.
∴y0=kx0-2==,
即P.
∵k≠0,
∴直线AP的斜率为
k 1==.
由MN⊥AP,得·k=-1,
∴2+2+6k2=6,解得k=±,
故直线方程为y=±x-2.
20.(本小题满分12分)(2010·诸城模拟)已知椭圆的中心在原点,焦点在x轴上,离心率为,且椭圆过圆C:x2+y2-4x+2y=0的圆心C.
(1)求椭圆的方程;
(2)设直线l过椭圆的焦点且与圆C相切,求直线l的方程.
解:(1)圆C的方程化为:(x-2)2+(y+)2=6.
圆心C(2,-),半径r=.
设椭圆的方程为+=1(a>b>0).
则⇒,
所以所求椭圆的方程是+=1.
(2)由(1)得椭圆的左右焦点分别是F1(-2,0),F2(2,0),
|F2C|==<r=,
F2在圆C内,故过F2没有圆C的切线,
设l的方程为y=k(x+2),即kx-y+2k=0.
点C(2,-)到直线l的距离为d=,
由d=,即=,
化简得5k2+4k-2=0,
解得k=或k=-,
故l的方程为x-5y+2=0或x+y+2=0.
19.(本小题满分12分)已知点(x,y)在曲线C上,将此点的纵坐标变为原来的2倍,对应的横坐标不变,得到的点满足方程x2+y2=8;定点M(2,1),平行于OM的直线l在y轴上的截距为m(m≠0),直线l与曲线C交于A,B两个不同点.
(1)求曲线C的方程;
(2)求m的取值范围.
解:(1)在曲线C上任取一个动点P(x,y),
则点(x,2y)在圆x2+y2=8上.
所以有x2+(2y)2=8.
整理得曲线C的方程为+=1.
(2)∵直线l平行于OM,且在y轴上的截距为m,
又kOM=,
∴直线l的方程为y=x+m.
由得x2+2mx+2m2-4=0
∵直线l与椭圆交于A、B两个不同点,
∴Δ=(2m)2-4(2m2-4)>0,
解得-2<m<2且m≠0.
∴m的取值范围是-2<m<0或0<m<2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com