4.(2009·浙江高考)若函数f(x)＝x²+(a∈R)，则下列结论正确的是　　　　　 (　)

A.∀a∈R，f(x) 在(0，+∞)上是增函数

B.∀a∈R，f(x)在(0，+∞)上是减函数

C.∃a∈R，f(x)是偶函数

D.∃a∈R，f(x)是奇函数

解析：当a＝16时，f(x)＝x²+，f′(x)＝2x－，

令f′(x)＞0得x＞2.

∴f(x)在(2，+∞)上是增函数，故A、B错.

当a＝0时，f(x)＝x²是偶函数，故C正确.

D显然错误.

答案：C

3.命题p：{2}∈{1,2,3}，q：{2}⊆{1,2,3}，则对复合命题的下述判断：①p或q为真；②p或q为假；③p且q为真；④p且q为假；⑤非p为真；⑥非q为假.其中判断正确的序号是　　.(填上你认为正确的所有序号)

解析：p：{2}∈{1,2,3}，q：{2}⊆{1,2,3}，p假q真，故①④⑤⑥正确.

答案：①④⑤⑥

2.下列各组命题中，满足“‘p或q’为真、‘p且q’为假、‘非p’为真”的是(　)

A.p：0＝∅；q：0∈∅

B.p：在△ABC中，若cos2A＝cos2B，则A＝B；q：y＝sinx在第一象限是增函数

C.p：a+b≥2(a，b∈R)；q：不等式|x|＞x的解集是(－∞，0)

D.p：圆(x－1)²+(y－2)²＝1的面积被直线x＝1平分；q：∀x∈{1，－1,0},2x+1＞0

解析：若要满足“‘p或q’为真，‘p且q’为假、‘非p’为真”，则p为假命题，q为真命题.A中p为假命题，q为假命题；B中p为真命题，q为假命题；C中p为假命题，q为真命题；D中p为真命题，q为假命题.

答案：C

1.设p、q是简单命题，则“p且q为假”是“p或q为假”的　　　　　　　　 (　)

A.必要不充分条件 　　　　　B.充分不必要条件

C.充要条件　 　　　　　　　　D.既不充分也不必要条件

解析：p且q为假，即p和q中至少有一个为假；p或q为假，即p和q都为假.

答案：A

12.设A＝{x|x²－ax+a²－19＝0}，B＝{x|x²－5x+6＝0}，C＝{x|x²+2x－8＝0}.

(1)A∩B＝A∪B，求a的值；

(2)∅ A∩B，且A∩C＝∅，求a的值；

(3)A∩B＝A∩C≠∅，求a的值.

解：(1)因为A∩B＝A∪B，所以A＝B，又由对应系数相等可得a＝5和a²－19＝6同时成立，即a＝5.

(2)由于B＝{2,3}，C＝{－4,2}，且∅A∩B，A∩C＝∅，故只可能3∈A.此时a²－3a－10＝0，

即a＝5或a＝－2，

由(1)可知，当a＝5时，A＝B＝{2,3}，

此时A∩C≠∅，与已知矛盾，所以a＝5舍去，故a＝－2.

(3)由于B＝{2,3}，C＝{－4,2}，且A∩B＝A∩C≠∅，

此时只可能2∈A，即a²－2a－15＝0，

也即a＝5或a＝－3，

由(2)可知a＝5不合题意，故a＝－3.

11.(文)(2009·北京高考)设A是整数集的一个非空子集.对于k∈A，如果k－1∉A，且k+

1∉A，那么称k是A的一个“孤立元”.给定S＝{1,2,3,4,5,6,7,8}，由S的3个元素构成的所有集合中，不含“孤立元”的集合共有　　个.

　 解析：依题可知，由S的3个元素构成的所有集合中，不含“孤立元”，这三个元素一定是相连的三个数.故这样的集合共有6个.

答案：6

(理)对任意两个集合M、N，定义：M－N＝{x|x∈M且x∉N}，M*N＝(M－N)∪(N－M)，设M＝{y|y＝x²，x∈R}，N＝{y|y＝3sinx，x∈R}，则M*N＝　　.

解析：依题意有M＝，

所以M－N＝(3，+∞)，N－M＝[－3,0)，

故M*N＝(M－N)∪(N－M)＝[－3,0)∪(3，+∞).

答案：[－3,0)∪(3，+∞)

10.设全集U＝A∪B＝{x∈N^*|lgx＜1}.若A∩(∁_UB)＝{m|m＝2n+1，n＝0,1,2,3,4}，则集合B＝　　.

解析：∵lgx＜1，∴0＜x＜10.

又∵x∈N^*，∴U＝A∪B＝{1,2,3，…，9}.

又∵A∩(∁_UB)＝{1,3,5,7,9}，

∴B＝{2,4,6,8}.

答案：{2,4,6,8}

9.(2009·江西高考)已知全集U＝A∪B中有m个元素，(∁_UA)∪(∁_UB)中有n个元素.若A∩B非空，则A∩B的元素个数为　　　　　　　　　　　　　　　　　　　　　 (　)

A.mn　　 　　　　B.m+n　　　　　 C.n－ m　　　　　 　D.m－n

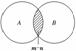解析：如图，U＝A∪B中有m个元素，

∵(∁_UA)∪(∁_UB)＝∁_U(A∩B)中有n个元素，

∴A∩B中有m－n个元素.

答案：D

8.(文)若集合A＝{x|(2x+1)(x－3)＜0}，B＝{x∈N^*|x≤5}，则A∩B是　　　 (　)

A.{1,2,3}　　　　　 B.{1,2}　　　　　 C.{4,5}　　　　　 D.{1,2,3,4,5}

解析：A＝{x|－＜x＜3}，B＝{1,2,3,4,5}，

∴A∩B＝{1,2}.

答案：B

(理)若集合A＝{x||2x－1|<3}，B＝，则A∩B是　　　 (　)

A.

B.{x|2<x<3}

C.

D.

解析：∵A＝{x|－2＜2x＜4}＝{x|－1＜x＜2}，

B＝{x|(2x+1)(x－3)＞0}＝{x|x＞3或x＜－}，

∴A∩B＝{x|－1＜x＜－}.

答案：D

7.(2010·东北师大附中模拟)设全集U是实数集R，M＝{x|x²＞4}，N＝{x|x≥3或x＜1}都是U的子集，则图中阴影部分所表示的集合是　　　　　　　　　　　　　 (　)

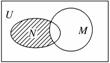
A.{x|－2≤x＜1}　　　 B.{x|－2≤x≤2}　　　 C.{x|1＜x≤2}　　　 D.{x|x＜2}

解析：图中阴影部分表示N∩(∁_UM)，

∵M＝{|x²>4}＝{x|x>2或x<－2}

∴∁_UM＝{x|－2≤x≤2}，∴N∩(∁_UM)＝{－2≤x＜1}.

答案：A