
题目列表(包括答案和解析)
6、已知函数 ,若
,若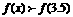 ,则
,则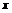 的取值范围为
的取值范围为
A、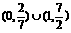 B、
B、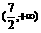 C、
C、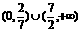 D、
D、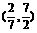
5、函数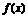 在(-1,1)上有定义且
在(-1,1)上有定义且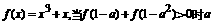 的取值范围为
的取值范围为
A、(-2,1) B、(0,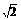 ) C、(0,1) D、(-2,
) C、(0,1) D、(-2,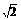 )
)
3、已知奇函数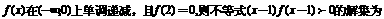
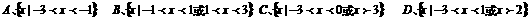 4、
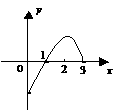
4、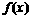 是定义在(0,3)上的函数,
是定义在(0,3)上的函数,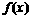 的图象如图所示,则不等式
的图象如图所示,则不等式 的解集 是
的解集 是
A.(0,1)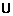 (2,3)B.
(2,3)B.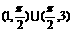
C.(0,1)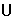
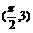 D.(0,1)
D.(0,1)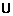 (1,3)
(1,3)
2、已知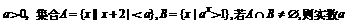 的取值范围为
的取值范围为
A、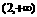 B(0,1) C、(0,1)
B(0,1) C、(0,1)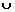
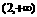 D、(0,1)
D、(0,1)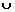
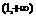
12.将一颗骰子先后抛掷两次,得到的点数分别记为a、b.
(1)求点P(a,b)落在区域内的概率;
(2)求直线ax+by+5=0与圆x2+y2=1不相切的概率.
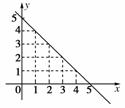
[解析] (1)先后两次抛掷一枚骰子,将得到的点数分别记为a,b,则事件总数为6×6=36.
∴表示的平面区域如图所示:
当a=1时,b=1,2,3,4
a=2时,b=1,2,3
a=3时,b=1,2
a=4时,b=1
共有(1,1),(1,2),…,(4,1)10种情况,
∴P==.
(2)∵直线ax+by+5=0与圆x2+y2=1相切的充要条件是=1,即a2+b2=25,
∵a、b∈{1,2,3,4,5,6},
满足条件的情况只有:a=3,b=4或a=4,b=3两种情况,
∴直线与圆相切的概率P==.
∴直线ax+by+5=0与圆x2+y2=1不相切的概率P=1-=.
11.袋子里装有30个小球,其中彩球中有n(n≥2)个红球、5个蓝球、10个黄球,其余为白球.若从袋子里取出3个都是相同颜色彩球的概率是,求红球的个数,并求从袋子中任取3个小球至少有1个是红球的概率.
[解析] 任取3个球的方法数为C=4 060.
设“3个球全为红球”为事件A,“3个球全为蓝球”为事件B,“3个球全为黄球”为事件C,则
P(B)==,P(C)==.
∵A、B、C为互斥事件,∴P(A+B+C)=P(A)+P(B)+P(C),即=P(A)++⇒P(A)=0.
∴红球的个数n≤2.又∵n≥2,故n=2.
记“3个球中至少有1个是红球”为事件D,则为“3个球中没有红球”,则P(D)=1-P()=1-=
10.一个口袋内有4个不同的红球和6个不同的白球,从中任取4个不同的球,试求红球的个数不比白球少的概率.
[解析] 从袋中任意取4个球,记恰有2个红球和2个白球、恰有3个红球和1个白球、全是红球依次为事件A,B,C,则P(A)=,P(B)=,P(C)=.
因为A,B,C彼此互斥,所以红球个数不比白球个数少的概率为
P(A+B+C)=P(A)+P(B)+P(C)=
(CC+CC+C)=.
∴红球的个数不比白球少的概率为.
9.中国乒乓球队甲、乙两名队员参加奥运会乒乓球女子单打比赛,甲夺得冠军的概率为,乙夺得冠军的概率为,那么中国队夺得女子乒乓球单打冠军的概率为________.
[解析] 设事件A为“甲夺得冠军”,事件B为“乙夺得冠军”,则P(A)=,P(B)=,因为事件A和事件B是互斥事件.∴P(A∪B)=P(A)+P(B)=+=.
[答案]
8.甲、乙两人下棋,甲获胜的概率为0.3,两人下成和棋的概率为0.5,那么甲不输的概率是________.
[解析] “甲获胜”记为事件A,“两人下成和棋”记为事件B,则易知A与B互斥,所以甲不输的概率为P(A∪B)=P(A)+P(B)=0.3+0.5=0.8.
[答案] 0.8
7.甲、乙两颗卫星同时监测台风,在同一时刻,甲、乙两颗卫星准确预报台风的概率分别为0.8和0.75,则在同一时刻至少有一颗卫星预报准确的概率为________.
[解析] 由对立事件的性质知在同一时刻至少有一颗卫星预报准确的概率为1-(1-0.8)(1-0.75)=0.95.
[答案] 0.95
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com