
题目列表(包括答案和解析)
3.下列判断中正确的是 ( )
A.△ABC中,a=7,b=14,A=30°,有两解
B.△ABC中,a=30,b=25,A=150°,有一解
C.△ABC中,a=6,b=9,A=45°,有两解
D.△ABC中,b=9,c=10,B=60°,无解
答案 B
2.(2008·福建理,10)在△ABC中,角A、B、C的对边分别为a、b、c,若(a2+c2-b2)tanB=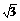 ac,则角B的值为( )
ac,则角B的值为( )
A.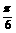 B.
B.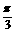 C.
C.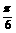 或
或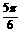 D.
D.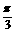 或
或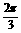
答案 D
1.(2008·陕西理,3)△ABC的内角A、B、C的对边分别为a、b、c,若c=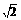 ,b=
,b= ,B=120°,则 a等于 ( )
,B=120°,则 a等于 ( )
A. B.2 C.
B.2 C.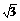 D.
D.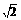
答案 D
9.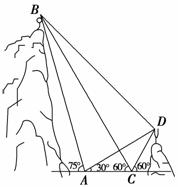 (2009年高考辽宁卷)如图,A、B、C、D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°、30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B、D间距离与另外哪两点间距离相等,然后求B、D的距离(计算结果精确到0.01
km,≈1.414,≈2.449).
(2009年高考辽宁卷)如图,A、B、C、D都在同一个与水平面垂直的平面内,B、D为两岛上的两座灯塔的塔顶,测量船于水面A处测得B点和D点的仰角分别为75°、30°,于水面C处测得B点和D点的仰角均为60°,AC=0.1 km.试探究图中B、D间距离与另外哪两点间距离相等,然后求B、D的距离(计算结果精确到0.01
km,≈1.414,≈2.449).
解:在△ACD中,∠DAC=30°,
∠ADC=60°-∠DAC=30°,
所以CD=AC=0.1.又∠BCD=180°-60°-60°=60°,
故CB是△CAD底边AD的中垂线,所以BD=BA.
在△ABC中,=,所以AB==.
同理,BD=≈0.33(km),
故B、D的距离约为0.33 km.
8.(原创题)在Rt△ABC中,斜边AB=2,内切圆的半径为r,则r的最大值为________.
解析:∵r==-1,∵4=a2+b2≥,∴(a+b)2≤8,∴a+b≤2,∴r≤-1.答案:-1
7.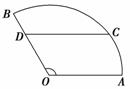 如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径为________米.
如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,C是该小区的一个出入口,且小区里有一条平行于AO的小路CD.已知某人从O沿OD走到D用了2分钟,从D沿着DC走到C用了3分钟.若此人步行的速度为每分钟50米,则该扇形的半径为________米.
解析:连结OC,在三角形OCD中,OD=100,CD=150,∠CDO=60°,由余弦定理可得OC2=1002+1502-2×100×150×=17500,∴OC=50.答案:50
6.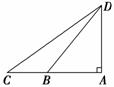 (2010年宁波十校联考)一船向正北方向匀速行驶,看见正西方向两座相距10海里的灯塔恰好与该船在同一直线上,继续航行半小时后,看见其中一座灯塔在南偏西60°方向上,另一灯塔在南偏西75°方向上,则该船的速度是________海里/小时.
(2010年宁波十校联考)一船向正北方向匀速行驶,看见正西方向两座相距10海里的灯塔恰好与该船在同一直线上,继续航行半小时后,看见其中一座灯塔在南偏西60°方向上,另一灯塔在南偏西75°方向上,则该船的速度是________海里/小时.
解析:假设该船从A处航行到了D处,两座灯塔分别在B、C位置,如图,设AD长为x,则AB=xtan60°,AC=xtan75°,所以BC=xtan75°-xtan60°=10,解得x=5,所以该船的速度v==10(海里/小时).答案:10
5.(2010年南京市高中联考)如图,海岸线上有相距5海里的两座灯塔A,B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°,与A相距3海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处.则两艘轮船之间的距离为________海里.
解析:连结AC.则AC=5,在△ACD中,AD=3,AC=5,∠DAC=45°,由余弦定理得CD=.答案:
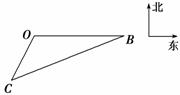
4.如图,位于港口O正东20海里B处的渔船回港时出现故障.位于港口南偏西30°,距港口10海里C处的拖轮接到海事部门营救信息后以30海里/小时的速度沿直线CB去营救渔船,则拖轮到达B处需要________小时.
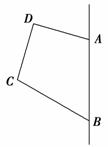 解析:由余弦定理得BC==10,从而需小时到达B处.答案:
解析:由余弦定理得BC==10,从而需小时到达B处.答案:
3. 为测量某塔AB的高度,在一幢与塔AB相距20 m的楼顶处测得塔顶A的仰角为30°,测得塔基B的俯角为45°,那么塔AB的高度是 ( )
A.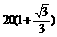 m B.
m B.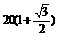 m C.
m C.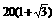 m D.30 m
m D.30 m
 答案 A
答案 A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com