
题目列表(包括答案和解析)
2.(2009年高考陕西卷改编)若3sinα+cosα=0,则的值为________.
解析:由3sinα+cosα=0得cosα=-3sinα,则===.
1.若tan(α+β)=,tan(β-)=,则tan(α+)=_____.
解析:tan(α+)=tan[(α+β)-(β-)]===.
6.已知角α∈(,),且(4cosα-3sinα)(2cosα-3sinα)=0.
(1)求tan(α+)的值;(2)求cos(-2α)的值.
解:∵(4cosα-3sinα)(2cosα-3sinα)=0,
又α∈(,),∴tanα=,sinα=,cosα=,
(1)tan(α+)===-7.
(2)cos2α=2cos2α-1=-,sin2α=2sinαcosα=,
cos(-2α)=coscos2α+sinsin2α=×(-)+×=.
B组
5.(原创题)函数f(x)=(sin2x+)(cos2x+)的最小值是________.
解析:f(x)=
=
=sin2xcos2x+-≥(-1).
4.(2009年高考上海卷)函数y=2cos2x+sin2x的最小值是__________________.
解析:y=2cos2x+sin2x=sin2x+1+cos2x=sin2x+cos2x+1
=sin(2x+)+1≥1-.
3.(2010年南京市调研)计算:=________.
解析:===.
2.已知π<θ<π,则 =________.
解析:∵π<θ<,∴<<,<<.
=
= =sin.
1.若sinα=,α∈(-,),则cos(α+)=________.
解析:由于α∈(-,),sinα=得cosα=,由两角和与差的余弦公式得:cos(α+)=-(cosα-sinα)=-.
15. (2008·广东五校联考)在△ABC中,角A、B、C的对边分别为a、b、c,已知a+b=5,c=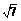 ,且4sin2
,且4sin2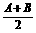 -cos2C=
-cos2C=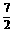 .
.
(1)求角C的大小;(2)求△ABC的面积.
解 (1)∵A+B+C=180°,由4sin2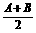 -cos2C=
-cos2C=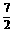 ,得4cos2
,得4cos2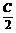 -cos2C=
-cos2C=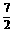 ,
,
∴4·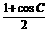 -(2cos2C-1)=
-(2cos2C-1)=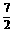 ,整理,得4cos2C-4cosC+1=0,解得cosC=
,整理,得4cos2C-4cosC+1=0,解得cosC=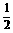 ,
,
∵0°<C<180°,∴C=60°.
(2)由余弦定理得c2=a2+b2-2abcosC,即7=a2+b2-ab,∴7=(a+b)2-3ab,
由条件a+b=5,得7=25-3ab,ab=6,∴S△ABC=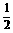 absinC=
absinC=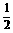 ×6×
×6× =
=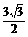 .
.
14. 已知△ABC的三个内角A、B、C的对边分别为a、b、c,若a、b、c成等差数列,且2cos2B-8cosB+5=0,求角B的大小并判断△ABC的形状.
解 方法一 ∵2cos2B-8cosB+5=0,∴2(2cos2B-1)-8cosB+5=0.
∴4cos2B-8cosB+3=0, 即(2cosB-1)(2cosB-3)=0.
解得cosB=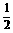 或cosB=
或cosB=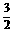 (舍去).∴cosB=
(舍去).∴cosB=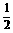 .∵0<B<
.∵0<B< ,∴B=
,∴B=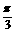 .
.
∵a,b,c成等差数列,∴a+c=2b.∴cosB=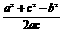 =
=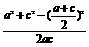 =
=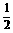 ,
,
化简得a2+c2-2ac=0,解得a=c.又∵B=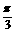 ,∴△ABC是等边三角形.
,∴△ABC是等边三角形.
方法二 ∵2cos2B-8cosB+5=0,∴2(2cos2B-1)-8cosB+5=0.
∴4cos2B-8cosB+3=0,即(2cosB-1)(2cosB-3)=0.
解得cosB=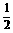 或cosB=
或cosB=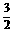 (舍去).∴cosB=
(舍去).∴cosB=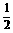 ,∵0<B<
,∵0<B< ,∴B=
,∴B=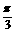 ,
,
∵a,b,c成等差数列,∴a+c=2b.由正弦定理得sinA+sinC=2sinB=2sin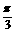 =
=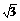 .
.
∴sinA+sin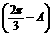 =
=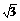 ,∴sinA+sin
,∴sinA+sin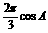 -cos
-cos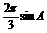 =
=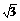 .
.
化简得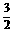 sinA+
sinA+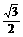 cosA=
cosA=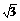 ,∴sin
,∴sin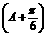 =1.
=1.
∴A+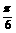 =
= ,∴A=
,∴A=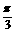 ,∴C=
,∴C=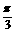 ,∴△ABC为等边三角形.
,∴△ABC为等边三角形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com