11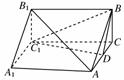．(2008年济宁模拟)如图，三棱柱ABC-A₁B₁C₁中，AA₁⊥平面ABC，BC⊥AC，BC＝AC＝2，AA₁＝3，D为AC的中点．

(1)求证：AB₁∥平面BDC₁；

(2)求二面角C₁-BD-C的余弦值；

(3)在侧棱AA₁上是否存在点P，使得CP⊥平面BDC₁？并证明你的结论．

[解析]　(1)证明：连结B₁C与BC₁相交于O，连接OD，如题图．

∵四边形BCC₁B₁是矩形，

∴O是B₁C的中点．

又D是AC的中点，

∴OD∥AB₁.

∵AB₁⊄平面BDC₁，OD⊂平面BDC₁，

∴AB₁∥平面BDC₁.

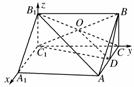
(2)如图建立空间直角坐标系，

则C₁(0,0,0)，B(0,3,2)，C(0,3,0)，A(2,3,0)，D(1,3,0)，＝(0,3,2)，＝(1,3,0)．

设n＝(x₁，y₁，z₁)是平面BDC₁的一个法向量，

则，即，

取x₁＝1，

则n＝(1，－，)．

易知＝(0,3,0)是平面ABC的一个法向量，

∴cos〈n，〉＝＝＝－.

又由题意可知二面角C₁-BD-C的余弦值为.

(3)假设侧棱AA₁上存在一点P(2，y,0)(0≤y≤3)，使得CP⊥平面BDC₁.

即，即，

∴.

∴方程组无解．∴假设不成立．

∴侧棱AA₁上不存在点P，使CP⊥平面BDC₁.

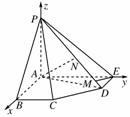
10．如图，在五棱锥P－ABCDE中，∠BAE＝90°，DE∥AB，PA＝AB＝AE＝2a，PB＝PE＝2a，BC＝DE＝a，求二面角A－PD－E的余弦值．

[解析]　由题意分析可知PA⊥AB，PA⊥AE，AB⊥AE，分别以AB，AE，AP所在直线为x，y，z轴建立如图所示的空间直角坐标系，

则B(2a,0,0)，E(0,2a,0)，P(0,0,2a)，

D(a,2a,0)，C(2a，a,0)．

过A作AN⊥PD于N.

∵P＝(a,2a，－2a)，设P＝λ，

∴A＝A+P＝(λa,2λa,2a－2λa)．

∵AN⊥PD，∴A·P＝0，

∴a·λa+2a·2λa－2a·(2a－2λa)＝0.

解得λ＝.∴A＝(a，a，a)，

即N＝(－a，－a，－a)．

同理，过E作EM⊥PD于M，

则M＝(－a，a，－a)．

二面角A－PD－E的大小为M，N所成的角〈M，N〉．

∵cos〈M，N〉＝，

∴二面角A－PD－E的余弦值为.

9．已知A(1,2,3)，B(2,1,2)，P(1,1,2)，点Q在直线OP上运动．当·取最小值时，点Q的坐标为________．

[解析]　设＝＝(λ，λ，2λ)，则＝(1－λ，2－λ，

3－2λ)，＝(2－λ，1－λ，2－2λ)．∴·＝(1－λ)·(2－λ)+(2－λ)(1－λ)+(3－2λ)(2－2λ)＝6λ²－16λ+10＝6²－.

∴当λ＝时·取最小值－，此时，＝，

即Q.

[答案]　

8．已知两点A(1，－2,3)，B(2,1，－1)，AB连线与xOz平面的交点为________．

[解析]　利用xOz平面上点的坐标为C(x,0，z)，求得点C分所成的比λ＝＝2，

∴x＝＝，z＝＝.

[答案]　

7．已知a＝(2，－1,3)，b＝(－4,2，x)，c＝(1，－x,2)．若(a+b)⊥c，则x＝________.

[解析]　a+b＝(－2,1,3+x)，(a+b)·c＝0，

∴－2－x+2(3+x)＝0，从而x＝－4.

[答案]　－4

6．(2010年银川模拟)已知长方体ABCD-A₁B₁C₁D₁中，AB＝BC＝4，CC₁＝2，则直线BC₁和平面DBB₁D₁所成角的正弦值为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　 D.

[解析]　如图建立空间直角坐标系，

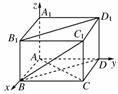则B(4,0,0)，C(4,4,0)，C₁(4,4,2)，

显然AC⊥平面BB₁D₁D，

∴＝(4,4,0)为平面BB₁D₁D的一个法向量．

又＝(0,4,2)，

∴cos〈，〉＝

＝＝.

即BC₁与平面BB₁D₁D所成角的正弦值为.故选C.

[答案]　C

5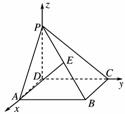．如图所示，PD垂直正方形ABCD所在平面，AB＝2，E为PB的中点，cos〈，〉＝.若以DA、DC、DP所在直线分别为x、y、z轴建立坐标系，则点E的坐标为(　)

A．(1,1,1)　 　　　　　　　　　　　　　　　　　　　　　 B.(2,1,1)

C.　 　　　　　　　　　　　　　　　　　　　　 D.

[解析]　A(2,0,0)、B(2,2,0)、C(0,2,0)，

令P(0,0,2m)(m>0)，

则E(1,1，m)，＝(－1,1，m)，＝(0,0,2m)，

∴cos〈，〉＝＝⇒m＝1.

∴E的坐标为(1,1,1)，故选择A.

[答案]　A

4．如图所示，正方体ABCD-A₁B₁C₁D₁中，M是棱DD₁的中点，点O为底面ABCD的中心，P为棱A₁B₁上任一点，则异面直线OP与AM所成的角的大小为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．随动点P的位置而定

[解析]　

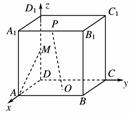[解析]　以D为原点，、、所在直线为x轴，y轴，z轴，建立空间直角坐标系，不妨设||＝1，则A(1,0,0)，M，

O设P点坐标为P(1 ，y,1)

＝(－1,0，)

＝(，y－，1)

∴·＝0，∴OP⊥AM.

[答案]　C

3．已知力F₁＝i+2j+3k，F₂＝－2i+3j－k，F₃＝3i－4j+5k，若F₁、F₂、F₃共同作用在一个物体上，使物体从点M₁(1，－2,1)移到点M₂(3,1,2)，则合力所做的功为(　)

A．10　 　　　　　　　　　　　　　　　　　　　　　　　　 B．12

C．14　 　　　　　　　　　　　　　　　　　　　　　　　　 D．16

[解析]　∵F＝F₁+F₂+F₃

＝(1,2,3)+(－2,3，－1)+(3，－4,5)＝(2,1,7)，

＝(2,3,1)，

∴F·＝(2,1,7)·(2,3,1)＝4+3+7＝14.

[答案]　C

2．(2010年白山模拟)向量a＝(2，－1,2)，与其共线且满足a·x＝－18的向量x是(　)

A．(，，－)　 　　　　　　　　　　　　　　　　　 B．(4，－2,4)

C．(－4,2，－4)　 　　　　　　　　　　　　　　　　　 D．(2，－3,4)

[解析]　设x＝(a，b，c)

∵x与a共线，∴(a，b，c)＝λ(2，－1,2)

∴a＝2λ，b＝－λ，c＝2λ

∴x＝(2λ，－λ，2λ)

又a·x＝－18

∴4λ+λ+4λ＝－18，∴λ＝－2

∴x＝(－4,2，－4)．

[答案]　C